Page 210 - How To Solve Word Problems In Calculus

P1: FYN/FZQ P2: FXS
PB056-07 Macros-FMT June 1, 2001 13:49 Char Count= 0

8
3 4/3
= y
4 0
3 4/3
= (8) − 0
4
= 12

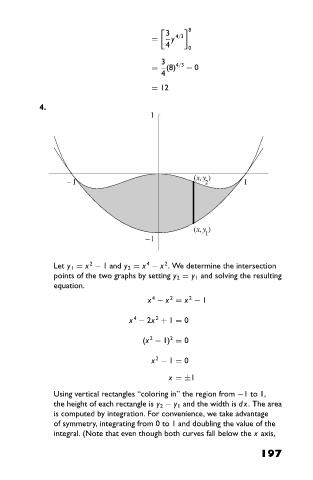
4.
1 1

− 1 (x,y ) 1 1
−1
2

(x,y )
1
−1

2
2
4
Let y 1 = x − 1 and y 2 = x − x . We determine the intersection
points of the two graphs by setting y 2 = y 1 and solving the resulting
equation.
4
2
2
x − x = x − 1
4
2
x − 2x + 1 = 0
2
2
(x − 1) = 0
2
x − 1 = 0
x =±1

Using vertical rectangles “coloring in” the region from −1to1,
the height of each rectangle is y 2 − y 1 and the width is dx. The area
is computed by integration. For convenience, we take advantage
of symmetry, integrating from 0 to 1 and doubling the value of the
integral. (Note that even though both curves fall below the x axis,

197