Page 88 - How To Solve Word Problems In Calculus

If a continuous function f has only one relative extremum
in an interval I at c, then
(a) If the relative extremum is a relative minimum, then
f has an absolute minimum at c.
(b) If the relative extremum is a relative maximum, then
f has an absolute maximum at c.

Note: If the interval I is closed, this theorem offers a conve-
nient alternative to the closed interval method.

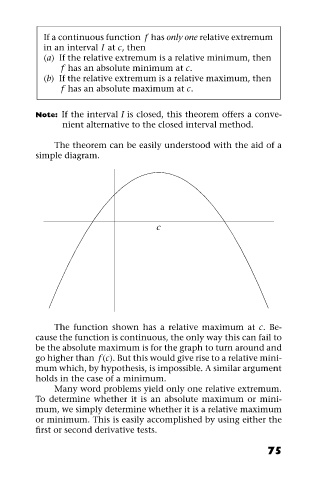
The theorem can be easily understood with the aid of a
simple diagram.

c

The function shown has a relative maximum at c. Be-
cause the function is continuous, the only way this can fail to
be the absolute maximum is for the graph to turn around and
go higher than f (c). But this would give rise to a relative mini-
mum which, by hypothesis, is impossible. A similar argument
holds in the case of a minimum.
Many word problems yield only one relative extremum.
To determine whether it is an absolute maximum or mini-
mum, we simply determine whether it is a relative maximum
or minimum. This is easily accomplished by using either the
first or second derivative tests.

75