Page 86 - How To Solve Word Problems In Calculus

we have a maximum but no minimum, or neither a maximum
nor a minimum. The only time we are guaranteed to have both
is when we have a continuous function on a closed interval.
Closely related to an absolute maximum is a relative (or
local) maximum.

A function f has a relative (or local) maximum at c if there
exists an open interval I containing c for which f (x) ≤ f (c)
for all x in I.

Of course, there is a corresponding definition for a relative
minimum. The only difference is that the inequality is re-
versed.
It can be shown that if f (x) has a relative extremum (max-
imum or minimum) at c, then c must be a critical number of
the function. But the converse is not true. A function may have
a critical value that corresponds to neither a maximum nor a
minimum.
2
3
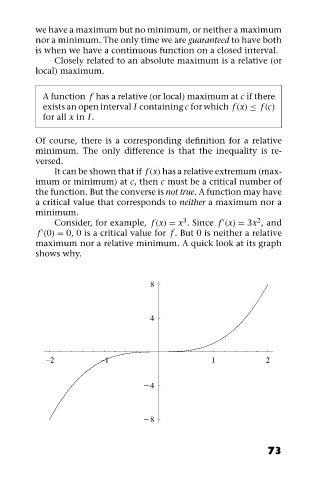
Consider, for example, f (x) = x . Since f (x) = 3x , and

f (0) = 0, 0 is a critical value for f . But 0 is neither a relative

maximum nor a relative minimum. A quick look at its graph
shows why.

8

4

2 1 1 2

4

8

73