Page 38 - Hydrogeology Principles and Practice

HYDC02 12/5/05 5:37 PM Page 21

Physical hydrogeology 21

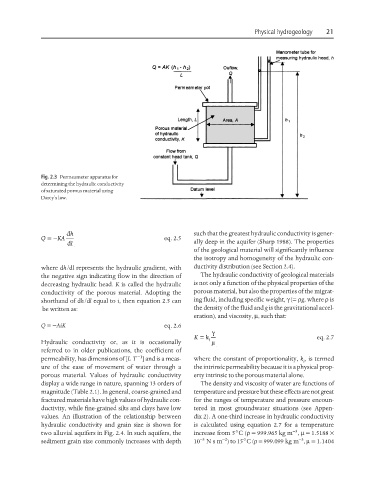
Fig. 2.3 Permeameter apparatus for
determining the hydraulic conductivity
of saturated porous material using
Darcy’s law.

Q =− KA h d eq. 2.5 such that the greatest hydraulic conductivity is gener-
l d ally deep in the aquifer (Sharp 1988). The properties
of the geological material will significantly influence
the isotropy and homogeneity of the hydraulic con-
where dh/dl represents the hydraulic gradient, with ductivity distribution (see Section 2.4).
the negative sign indicating flow in the direction of The hydraulic conductivity of geological materials
decreasing hydraulic head. K is called the hydraulic is not only a function of the physical properties of the
conductivity of the porous material. Adopting the porous material, but also the properties of the migrat-
shorthand of dh/dl equal to i, then equation 2.5 can ing fluid, including specific weight, γ (= ρg, where ρ is
be written as: the density of the fluid and g is the gravitational accel-
eration), and viscosity, µ, such that:
Q =−AiK eq. 2.6
γ
=
K k i eq. 2.7
Hydraulic conductivity or, as it is occasionally µ

referred to in older publications, the coefficient of
−1
permeability, has dimensions of [LT ] and is a meas- where the constant of proportionality, k , is termed
i
ure of the ease of movement of water through a the intrinsic permeability because it is a physical prop-
porous material. Values of hydraulic conductivity erty intrinsic to the porous material alone.
display a wide range in nature, spanning 13 orders of The density and viscosity of water are functions of
magnitude (Table 2.1). In general, coarse-grained and temperature and pressure but these effects are not great
fractured materials have high values of hydraulic con- for the ranges of temperature and pressure encoun-
ductivity, while fine-grained silts and clays have low tered in most groundwater situations (see Appen-
values. An illustration of the relationship between dix 2). A one-third increase in hydraulic conductivity
hydraulic conductivity and grain size is shown for is calculated using equation 2.7 for a temperature
−3
two alluvial aquifers in Fig. 2.4. In such aquifers, the increase from 5°C (ρ = 999.965 kg m , µ = 1.5188 ×
−3
−3
−2
sediment grain size commonly increases with depth 10 Nsm ) to 15°C (ρ = 999.099 kg m , µ = 1.1404