Page 117 - Innovations in Intelligent Machines

UAV Path Planning Using Evolutionary Algorithms 107

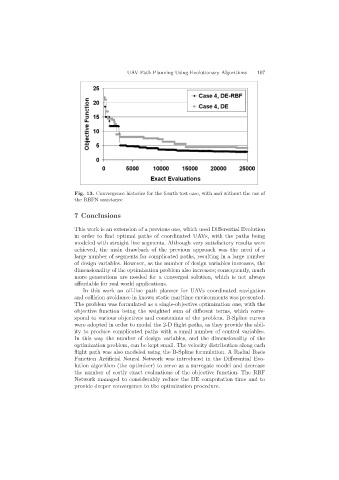
Fig. 13. Convergence histories for the fourth test case, with and without the use of
the RBFN assistance

7 Conclusions

This work is an extension of a previous one, which used Differential Evolution
in order to find optimal paths of coordinated UAVs, with the paths being
modeled with straight line segments. Although very satisfactory results were
achieved, the main drawback of the previous approach was the need of a
large number of segments for complicated paths, resulting in a large number
of design variables. However, as the number of design variables increases, the
dimensionality of the optimization problem also increases; consequently, much
more generations are needed for a converged solution, which is not always
affordable for real world applications.
In this work an off-line path planner for UAVs coordinated navigation
and collision avoidance in known static maritime environments was presented.
The problem was formulated as a single-objective optimization one, with the
objective function being the weighted sum of different terms, which corre-
spond to various objectives and constraints of the problem. B-Spline curves
were adopted in order to model the 2-D flight paths, as they provide the abil-
ity to produce complicated paths with a small number of control variables.
In this way the number of design variables, and the dimensionality of the
optimization problem, can be kept small. The velocity distribution along each
flight path was also modeled using the B-Spline formulation. A Radial Basis
Function Artificial Neural Network was introduced in the Differential Evo-
lution algorithm (the optimizer) to serve as a surrogate model and decrease
the number of costly exact evaluations of the objective function. The RBF
Network managed to considerably reduce the DE computation time and to
provide deeper convergence to the optimization procedure.