Page 196 - Introduction to Continuum Mechanics
P. 196
Symmetry of Stress Tensor- Principle of Moment of Momentum 181
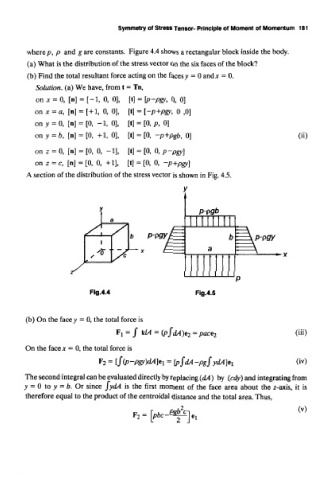
where p, p and g are constants. Figure 4.4 shows a rectangular block inside the body.
(a) What is the distribution of the stress vector on the six faces of the block?
(b) Find the total resultant force acting on the faces y = 0 and x = 0.
Solution, (a) We have, from t = Tn,
A section of the distribution of the stress vector is shown in Fig. 4.5.
Fig.4.4 Fig.4.5
(b) On the facey = 0, the total force is
On the face x = 0, the total force is
The second integral can be evaluated directly by replacing (dA) by (cdy) and integrating from
y = 0 to y = b. Or since jydA is the first moment of the face area about the z-axis, it is
therefore equal to the product of the centroidal distance and the total area. Thus,