Page 288 - Introduction to Information Optics

5.6. Wigner Distribution Function

(a) (b) CO

(Oft

(c) (d) CO
A

7 7

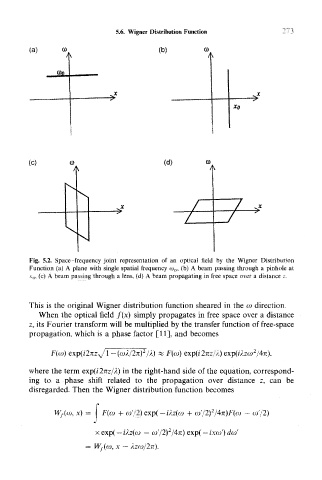
Fig. 5.2. Space -frequency joint representation of an optical field by the Wigner Distribution
Function (a) A plane with single spatial frequency o> 0, (b) A beam passing through a pinhole at
x 0, (c) A beam passing through a lens, (d) A beam propagating in free space over a distance z.

This is the original Wigner distribution function sheared in the a> direction.
When the optical field /(x) simply propagates in free space over a distance
z, its Fourier transform will be multiplied by the transfer function of free-space
propagation, which is a phase factor [11], and becomes

2
F(OJ) exp(i'27tz v/l —((OA/2n) /A) « F(w) i
where the term exp(i 2nz/A) in the right-hand side of the equation, correspond-
ing to a phase shift related to the propagation over distance z, can be
disregarded. Then the Wigner distribution function becomes
f
2
W f(w, x) = F(co + co'/2) exp(-Uz(co + a)'/2) /4n)F(co - w'/2)
2
x exp( — iAz(o) — a)'/2) /4n) exp( — ixa>') d(D r
W f(co, x — Az(a/2n).