Page 290 - Introduction to chemical reaction engineering and kinetics

10.4 Inhibition and Activation in Enzyme Reactions 271

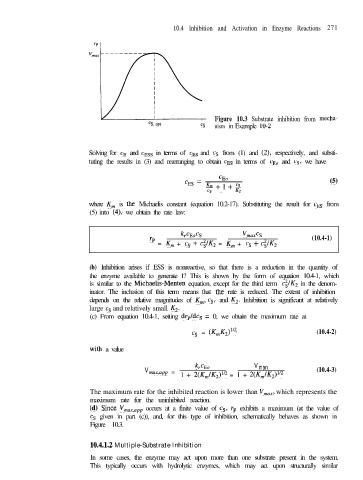
Figure 10.3 Substrate inhibition from mecha-
cs nism in Example 10-2

Solving for cn and cnss in terms of cEs and cs from (1) and (2), respectively, and substi-
tuting the results in (3) and rearranging to obtain ens in terms of cEO and cs, we have

(5)

where Km is the Michaelis constant (equation 10.2-17). Substituting the result for cus from
(5) into (4) we obtain the rate law:

k&E&S VnzaxCS (10.4-1)
‘-’ = K,,, + cs + c;lK, = K,,, + cs + c;lK,

(b) Inhibition arises if ESS is nonreactive, so that there is a reduction in the quantity of
the enzyme available to generate I? This is shown by the form of equation 10.4-1, which
is similar to the Michaelis-Menten equation, except for the third term c:lK, in the denom-
inator. The inclusion of this term means that the rate is reduced. The extent of inhibition
depends on the relative magnitudes of Km, cs, and K2. Inhibition is significant at relatively
large cs and relatively small K2.
(c) From equation 10.4-1, setting drrldc, = 0, we obtain the maximum rate at

cs = (KmK2)“2 (10.4-2)

with a value

V max,app = k&EC3 V man (10.4-3)
1 + 2(K,,JK,)‘” = 1 + 2(K,lK,)‘”

The maximum rate for the inhibited reaction is lower than Vmax, which represents the
maximum rate for the uninhibited reaction.
(4 Since Vmax,app occurs at a finite value of cs, r, exhibits a maximum (at the value of
cs given in part (c)), and, for this type of inhibition, schematically behaves as shown in
Figure 10.3.

10.4.1.2 Multiple-Substrate Inhibition
In some cases, the enzyme may act upon more than one substrate present in the system.
This typically occurs with hydrolytic enzymes, which may act upon structurally similar