Page 159 - Lindens Handbook of Batteries

6.12 PRINCIPLES OF OPERATION

0.7 4.2
Data 4.1 Data
0.6 Fit Fit
4
0.5 3.9
3.8
0.4
E n (V) E p (V) 3.7
0.3
3.6
0.2 3.5
3.4
0.1
3.3
0 3.2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x y
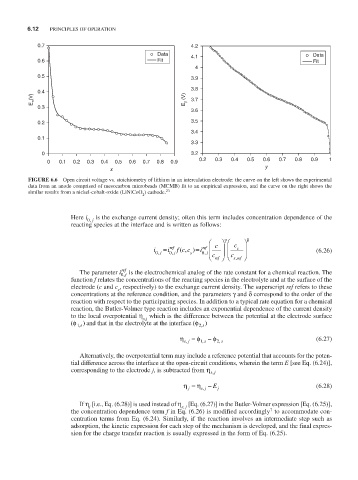
FiguRE 6.6 Open circuit voltage vs. stoichiometry of lithium in an intercalation electrode: the curve on the left shows the experimental
data from an anode comprised of mesocarbon microbeads (MCMB) fit to an empirical expression, and the curve on the right shows the
similar results from a nickel-cobalt-oxide (LiNiCoO ) cathode. 23
2

Here i is the exchange current density; often this term includes concentration dependence of the
0, j
reacting species at the interface and is written as follows:

γ
 c   c  δ
ref
i 0, j i = 0, j fc c )= (, s i 0, ref j     s   (6.26)
 
 c ref   c sreef 
,
ref
The parameter i is the electrochemical analog of the rate constant for a chemical reaction. The
0,
j
function f relates the concentrations of the reacting species in the electrolyte and at the surface of the
electrode (c and c , respectively) to the exchange current density. The superscript ref refers to these
s
concentrations at the reference condition, and the parameters γ and δ correspond to the order of the
reaction with respect to the participating species. In addition to a typical rate equation for a chemical
reaction, the Butler-Volmer type reaction includes an exponential dependence of the current density
to the local overpotential η which is the difference between the potential at the electrode surface
s,j
(φ , 1 s ) and that in the electrolyte at the interface (φ , 2 s )
η sj , = φ s , 1 - φ s , 2 (6.27)
Alternatively, the overpotential term may include a reference potential that accounts for the poten-
tial difference across the interface at the open-circuit conditions, wherein the term E [see Eq. (6.24)],
corresponding to the electrode j, is subtracted from η sj ,
η j η = s j , - E (6.28)
j

If η [i.e., Eq. (6.28)] is used instead of η [Eq. (6.27)] in the Butler-Volmer expression [Eq. (6.25)],
s, j
j
7
the concentration dependence term f in Eq. (6.26) is modified accordingly to accommodate con-
centration terms from Eq. (6.24). Similarly, if the reaction involves an intermediate step such as
adsorption, the kinetic expression for each step of the mechanism is developed, and the final expres-
sion for the charge transfer reaction is usually expressed in the form of Eq. (6.25).