Page 169 - Macromolecular Crystallography

158 MACROMOLECULAR CRYS TALLOGRAPHY

(a) (b) (c)

Target distance

Interatomic Rotamer angle
distance Rotamer angle
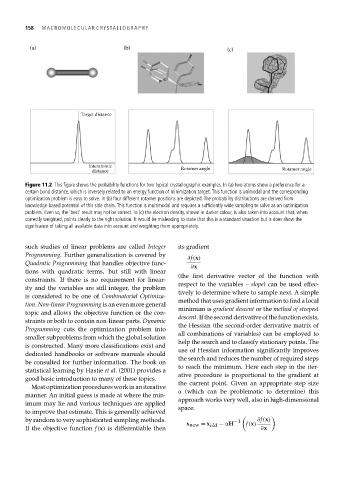
Figure 11.2 This figure shows the probability functions for two typical crystallographic examples. In (a) two atoms show a preference for a
certain bond distance, which is inversely related to an energy function of minimization target. This function is unimodal and the corresponding
optimization problem is easy to solve. In (b) four different rotamer positions are depicted. The probability distributions are derived from
knowledge-based potential of this side chain. This function is multimodal and requires a sufficiently wide sampling to solve as an optimization
problem. Even so, the ‘best’ result may not be correct. In (c) the electron density, shown in darker colour, is also taken into account that, when
correctly weighted, points clearly to the right solution. It would be misleading to state that this is a standard situation but is does show the
significance of taking all available data into account and weighting them appropriately.

such studies of linear problems are called Integer its gradient
Programming. Further generalization is covered by
∂f(x)
Quadratic Programming that handles objective func-
∂x
tions with quadratic terms, but still with linear
(the first derivative vector of the function with
constraints. If there is no requirement for linear-
respect to the variables – slope) can be used effec-
ity and the variables are still integer, the problem
tively to determine where to sample next. A simple
is considered to be one of Combinatorial Optimiza-
method that uses gradient information to find a local
tion. Non-linear Programming is an even more general
minimum is gradient descent or the method of steepest
topic and allows the objective function or the con-
descent. Ifthesecondderivativeofthefunctionexists,
straints or both to contain non-linear parts. Dynamic
the Hessian (the second-order derivative matrix of
Programming cuts the optimization problem into
all combinations of variables) can be employed to
smaller subproblems from which the global solution
help the search and to classify stationary points. The
is constructed. Many more classifications exist and
use of Hessian information significantly improves
dedicated handbooks or software manuals should
the search and reduces the number of required steps
be consulted for further information. The book on
to reach the minimum. Here each step in the iter-
statistical learning by Hastie et al. (2001) provides a
ative procedure is proportional to the gradient at
good basic introduction to many of these topics.
the current point. Given an appropriate step size
Most optimization procedures work in an iterative
α (which can be problematic to determine) this
manner. An initial guess is made at where the min-
approach works very well, also in high-dimensional
imum may lie and various techniques are applied
space:
to improve that estimate. This is generally achieved

by random to very sophisticated sampling methods. −1 ∂f(x)
x new = x old − αH f(x)
If the objective function f(x) is differentiable then ∂x