Page 172 - Macromolecular Crystallography

MODEL BUILDING, REFINEMENT, AND VALIDATION 161

goal of maximizing the agreement between the mea- experimental diffraction data extending to at least
sured experimental diffraction data and predicted atomic resolution (about 1.2 Å) are necessary to pro-
structure factors from the model. At the same time, vide a sufficient number of reflections and thus
they optimize the agreement to a variety of a priori a high enough observation-to-parameter ratio to
available information, most commonly the stereo- justify an atomic model. The dependence of the
chemistry of the model. The objective function for observation-to-parameter ratio is exemplified in
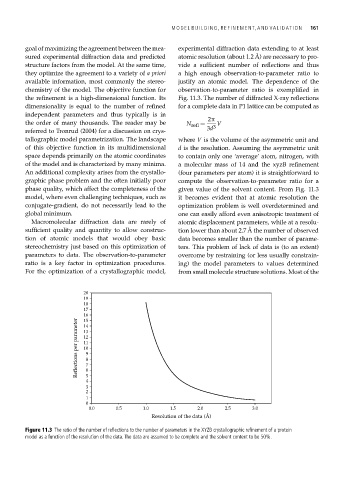
the refinement is a high-dimensional function. Its Fig. 11.3. The number of diffracted X-ray reflections
dimensionality is equal to the number of refined for a complete data in P1 lattice can be computed as
independent parameters and thus typically is in
2π
the order of many thousands. The reader may be N refl = 3 V
referred to Tronrud (2004) for a discussion on crys- 3d
tallographic model parametrization. The landscape where V is the volume of the asymmetric unit and
of this objective function in its multidimensional d is the resolution. Assuming the asymmetric unit
space depends primarily on the atomic coordinates to contain only one ‘average’ atom, nitrogen, with
of the model and is characterized by many minima. a molecular mass of 14 and the xyzB refinement
An additional complexity arises from the crystallo- (four parameters per atom) it is straightforward to
graphic phase problem and the often initially poor compute the observation-to-parameter ratio for a
phase quality, which affect the completeness of the given value of the solvent content. From Fig. 11.3
model, where even challenging techniques, such as it becomes evident that at atomic resolution the
conjugate-gradient, do not necessarily lead to the optimization problem is well overdetermined and
global minimum. one can easily afford even anisotropic treatment of
Macromolecular diffraction data are rarely of atomic displacement parameters, while at a resolu-
sufficient quality and quantity to allow construc- tion lower than about 2.7 Å the number of observed
tion of atomic models that would obey basic data becomes smaller than the number of parame-
stereochemistry just based on this optimization of ters. This problem of lack of data is (to an extent)
parameters to data. The observation-to-parameter overcome by restraining (or less usually constrain-
ratio is a key factor in optimization procedures. ing) the model parameters to values determined
For the optimization of a crystallographic model, from small molecule structure solutions. Most of the

20
19
18
17
16
Reflections per parameter 13 9 8
15
14
12
11
10

4 7 6 5
3
2
1
0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
Resolution of the data (Å)
Figure 11.3 The ratio of the number of reflections to the number of parameters in the XYZB crystallographic refinement of a protein
model as a function of the resolution of the data. The data are assumed to be complete and the solvent content to be 50%.