Page 235 - Master Handbook of Acoustics

second, a far cry from the 1,000 per second desired. One solution is to arrange many simple
reverberators in parallel. Four such simple reverberators, arranged in parallel, might produce 4 × 25
= 100 echoes per second. It would require 40 such reverberators in parallel to achieve the required
echo density.

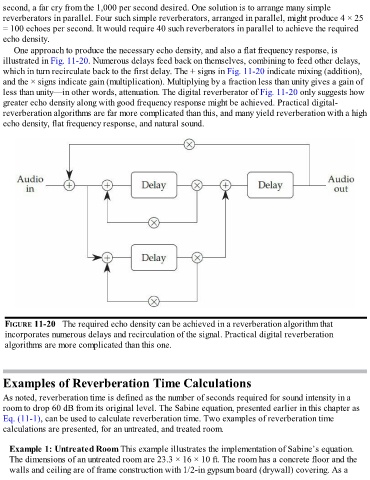
One approach to produce the necessary echo density, and also a flat frequency response, is
illustrated in Fig. 11-20. Numerous delays feed back on themselves, combining to feed other delays,
which in turn recirculate back to the first delay. The + signs in Fig. 11-20 indicate mixing (addition),
and the × signs indicate gain (multiplication). Multiplying by a fraction less than unity gives a gain of
less than unity—in other words, attenuation. The digital reverberator of Fig. 11-20 only suggests how
greater echo density along with good frequency response might be achieved. Practical digital-

reverberation algorithms are far more complicated than this, and many yield reverberation with a high
echo density, flat frequency response, and natural sound.

FIGURE 11-20 The required echo density can be achieved in a reverberation algorithm that
incorporates numerous delays and recirculation of the signal. Practical digital reverberation
algorithms are more complicated than this one.

Examples of Reverberation Time Calculations

As noted, reverberation time is defined as the number of seconds required for sound intensity in a

room to drop 60 dB from its original level. The Sabine equation, presented earlier in this chapter as
Eq. (11-1), can be used to calculate reverberation time. Two examples of reverberation time
calculations are presented, for an untreated, and treated room.

Example 1: Untreated Room This example illustrates the implementation of Sabine’s equation.
The dimensions of an untreated room are 23.3 × 16 × 10 ft. The room has a concrete floor and the
walls and ceiling are of frame construction with 1/2-in gypsum board (drywall) covering. As a