Page 41 - Master Handbook of Acoustics

up to some point at which energy begins to fall off due to generator limitations. Random noise may be
considered as statistically distributed signals with a continuous frequency spectrum.

For a sine wave, all the energy is concentrated at one frequency. The sine wave produced by this
particular signal generator is not really a pure sine wave. No oscillator is perfect and all have some
harmonic content, but in scanning the spectrum of this sine wave, the harmonics measured were too

low to show on the graph scale of Fig. 1-13A.
The triangular waveform of this signal generator has a major fundamental component of 10 unit’s
magnitude, as shown in Fig. 1-13B. The waveform analyzer has detected a significant second
harmonic component at f , twice the frequency of the fundamental with a magnitude of 0.21 units. The
2
third harmonic shows an amplitude of 1.13 units, the fourth of 0.13 units, and so on. The seventh
harmonic has an amplitude of 0.19 units and the fourteenth harmonic (about 15 kHz in this case) has
an amplitude of 0.03 units, but is still easily detectable. We see that this triangular waveform has both
odd and even components of modest amplitude through the audible spectrum. If we know the
amplitude and phases of each of these, the original triangular waveform can be synthesized by

combining them.
A comparable analysis reveals the spectrum of the square wave shown in Fig. 1-13C. It has
harmonics of far greater amplitude than the triangular waveform with a distinct tendency toward more
prominent odd than even harmonics. The third harmonic shows an amplitude 34% of the fundamental.
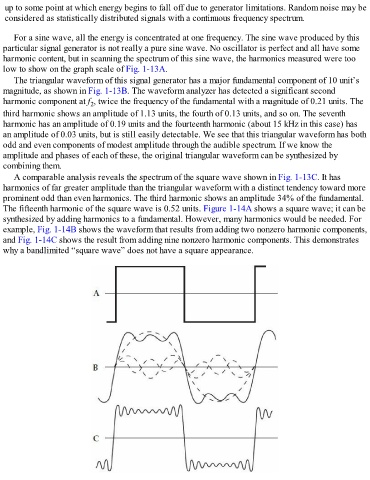
The fifteenth harmonic of the square wave is 0.52 units. Figure 1-14A shows a square wave; it can be
synthesized by adding harmonics to a fundamental. However, many harmonics would be needed. For

example, Fig. 1-14B shows the waveform that results from adding two nonzero harmonic components,
and Fig. 1-14C shows the result from adding nine nonzero harmonic components. This demonstrates
why a bandlimited “square wave” does not have a square appearance.