Page 45 - Master Handbook of Acoustics

decibels, which are based on ratios.
Ratios of powers, or ratios of intensities, or ratios of sound pressure, voltage, current, or anything
else are dimensionless. For example, the ratio of 1 W to 100 W is 1 W/100 W, and the watt unit in the

numerator and the watt unit in the denominator cancel, leaving, a pure number without dimension.
This is important in our discussion of decibels because decibels use logarithms and logarithms can
only be taken of nondimensional numbers.

Expressing Numbers

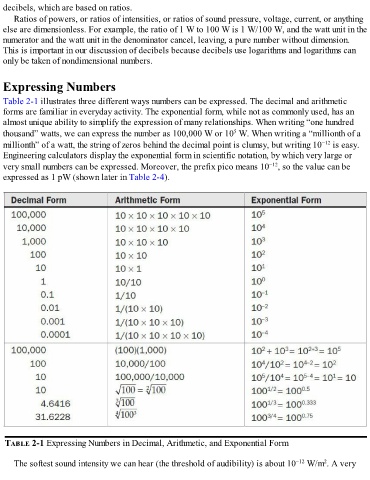
Table 2-1 illustrates three different ways numbers can be expressed. The decimal and arithmetic
forms are familiar in everyday activity. The exponential form, while not as commonly used, has an
almost unique ability to simplify the expression of many relationships. When writing “one hundred

5
thousand” watts, we can express the number as 100,000 W or 10 W. When writing a “millionth of a
−12
millionth” of a watt, the string of zeros behind the decimal point is clumsy, but writing 10 is easy.
Engineering calculators display the exponential form in scientific notation, by which very large or

−12
very small numbers can be expressed. Moreover, the prefix pico means 10 , so the value can be
expressed as 1 pW (shown later in Table 2-4).

TABLE 2-1 Expressing Numbers in Decimal, Arithmetic, and Exponential Form

2
−12
The softest sound intensity we can hear (the threshold of audibility) is about 10 W/m . A very