Page 30 - Mathematical Models and Algorithms for Power System Optimization

20 Chapter 2

2.3.1 Notations

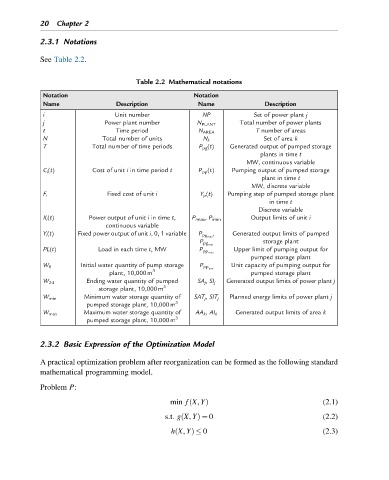
See Table 2.2.

Table 2.2 Mathematical notations
Notation Notation
Name Description Name Description
i Unit number NP Set of power plant j
j Power plant number N PLANT Total number of power plants
t Time period N AREA T number of areas
N Total number of units N k Set of area k
T Total number of time periods P pg (t) Generated output of pumped storage
plants in time t
MW, continuous variable
Cost of unit i in time period t
C i (t) P pp (t) Pumping output of pumped storage
plant in time t
MW, discrete variable
Fixed cost of unit i
F i Y p (t) Pumping step of pumped storage plant
in time t
Discrete variable
Output limits of unit i
X i (t) Power output of unit i in time t, P imax , P imin
continuous variable
Y i (t) Fixed power output of unit i, 0, 1 variable P pg max , Generated output limits of pumped
storage plant
P pg min
PL(t) Load in each time t,MW P pp max Upper limit of pumping output for
pumped storage plant
Initial water quantity of pump storage P pp unt Unit capacity of pumping output for
W 0
3
plant, 10,000m pumped storage plant
SA j , SI j Generated output limits of power plant j
Ending water quantity of pumped
W 24
3
storage plant, 10,000m
SAT j , SIT j Planned energy limits of power plant j
Minimum water storage quantity of
W min
3
pumped storage plant, 10,000m
Generated output limits of area k
AA k , AI k
Maximum water storage quantity of
W max
3
pumped storage plant, 10,000m
2.3.2 Basic Expression of the Optimization Model
A practical optimization problem after reorganization can be formed as the following standard
mathematical programming model.
Problem P:
min fX, YÞ (2.1)
ð
s:t: gX, YÞ ¼ 0 (2.2)
ð
hX, YÞ 0 (2.3)
ð