Page 468 - Mathematical Techniques of Fractional Order Systems

454 Mathematical Techniques of Fractional Order Systems

1

0.8
0.6

0.4

0.2
y 2 0

–0.2

–0.4
–0.6

–0.8
–1
–1.5 –1 –0.5 0 0.5 1 1.5
y 1

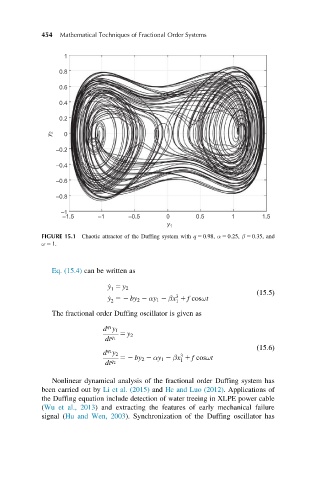
FIGURE 15.1 Chaotic attractor of the Duffing system with q 5 0:98, α 5 0:25, β 5 0:35, and
ω 5 1.

Eq. (15.4) can be written as

_ y 5 y 2
1
ð15:5Þ
3
_ y 52 by 2 2 αy 1 2 βx 1 f cosωt
2
1
The fractional order Duffing oscillator is given as
q 1
d y 1
5 y 2
q
dt 1
ð15:6Þ
q 2
d y 2 3
52 by 2 2 αy 1 2 βx 1 f cosωt
q 1
dt 2
Nonlinear dynamical analysis of the fractional order Duffing system has
been carried out by Li et al. (2015) and He and Luo (2012). Applications of
the Duffing equation include detection of water treeing in XLPE power cable
(Wu et al., 2013) and extracting the features of early mechanical failure
signal (Hu and Wen, 2003). Synchronization of the Duffing oscillator has