Page 539 - Mathematical Techniques of Fractional Order Systems

Chaotic Properties of Various Types of Hidden Attractors Chapter | 17 519

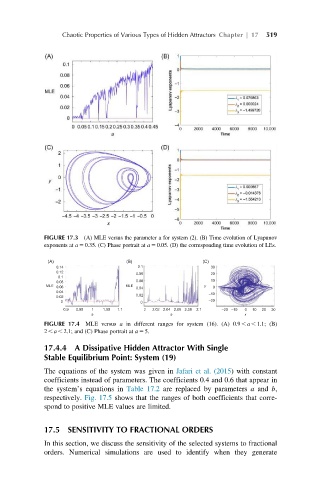
FIGURE 17.3 (A) MLE versus the parameter a for system (2). (B) Time evolution of Lyapunov
exponents at a 5 0.35. (C) Phase portrait at a 5 0.05. (D) the corresponding time evolution of LEs.

(A) (B) (C)
0.14 0.1 30
0.12
0.08 20
0.1
0.08 0.06 10
MLE 0.06 MLE 0.04 y 0
0.04
0.02 –10
0.02
0 0 –20
0.9 0.95 1 1.05 1.1 2 2.02 2.04 2.06 2.08 2.1 –20 –10 0 10 20 30
a a x
FIGURE 17.4 MLE versus a in different ranges for system (16). (A) 0.9 , a , 1.1; (B)
2 , a , 2.1; and (C) Phase portrait at a 5 5.
17.4.4 A Dissipative Hidden Attractor With Single
Stable Equilibrium Point: System (19)
The equations of the system was given in Jafari et al. (2015) with constant
coefficients instead of parameters. The coefficients 0.4 and 0.6 that appear in
the system’s equations in Table 17.2 are replaced by parameters a and b,
respectively. Fig. 17.5 shows that the ranges of both coefficients that corre-
spond to positive MLE values are limited.

17.5 SENSITIVITY TO FRACTIONAL ORDERS
In this section, we discuss the sensitivity of the selected systems to fractional
orders. Numerical simulations are used to identify when they generate