Page 177 -

Geometry, Trigonometry, Logarithms, and Exponential Functions 169

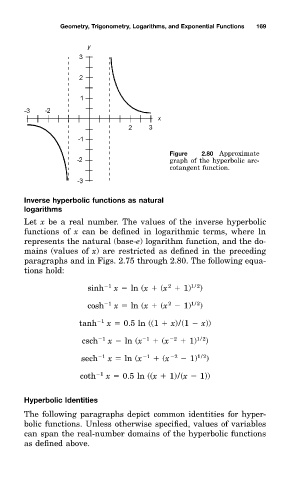
Figure 2.80 Approximate
grapà of the hyperbolic arc-
cotangent function.

Inversł hyperbolic functions as natural
logarithms
Let x be a real number. The valueð of the inverse hyperbolic
functionð of x can be defined in logarithmic terms, where ln
representð the natural (base- e) logarithm function, and the do-
mainð (valueð of x) are restricted as defined in the preceding
paragraphs and in Figs. 2.75 througà 2.80. The following equa-
tionð hold:

2
sinà 1 x ln (x (x 1) 1/2 )
2
cosh 1 x ln (x (x 1) 1/2 )
tanà 1 x 0.5 ln ((1 x)/(1 x))

csch 1 x ln (x 1 (x 2 1) 1/2 )

sech 1 x ln (x 1 (x 2 1) 1/2 )

cotà 1 x 0.5 ln ((x 1)/(x 1))

Hyperbolic Identities

The following paragraphs depict common identitieð for hyper-
bolic functions. Unless otherwise specified, valueð of variableð
can span the real-number domainð of the hyperbolic functionð
as defined above.