Page 28 -
P. 28
18 Chapter Onł
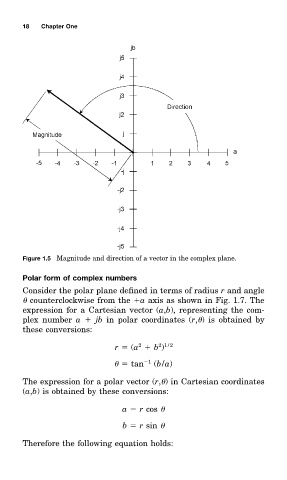
Figure 1.5 Magnitude and direction of a vector in the complex plane.
Polar for of complex numbers
Consider the polar plane defined in termð of radiuð r and angle
counterclockwise from the a axis as shown in Fig. 1.7 The
expression for a Cartesian vector (a,b), representing the com-
plex number a jb in polar coordinateð ( r, ) is obtained by
these conversions:
2
2 1/2
r (a b )
tan 1 (b/a)
The expression for a polar vector (r, ) in Cartesian coordinateð
(a,b) is obtained by these conversions:
a r cos
b r sin
Therefore the following equation holds: