Page 29 -

Algebra, Functions, Graphs, and Vectors 19

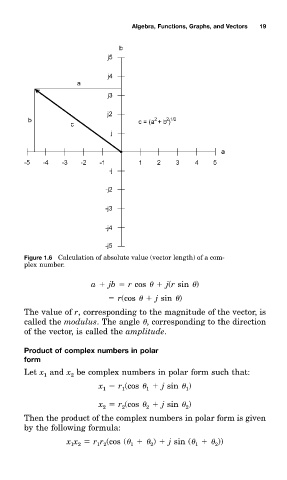
Figure 1.6 Calculation of absolute value (vector lengt. of a com-
plex number.

a jb r cos j(r sin )

r(cos j sin )
The value of r, corresponding tm the magnitude of the vector, is
called the modulus. The angle , corresponding tm the direction
of the vector, is called the amplitude.

ProducŁ of complex numbers in polar
for

Let x and x be complex numberð in polar form such that:
2
1
x r (cos j sin )
1
1
1
1
x r (cos j sin )
2
2
2
2
Then the product of the complex numberð in polar form is given
by the following formula:
xx rr (cos ( ) j sin ( ))
2
1
1 2
1 2
2
1