Page 72 - Mechanical Engineers' Handbook (Volume 4)

6 Fluid Energy 61

n
3
udA
1
A
u 1
3
i
3
3
VA Vn i 1
For laminar flow in a pipe, 2; for turbulent flow in a pipe, 1.05–1.06; and if one-
dimensional flow is assumed, 1.
For one-dimensional flow of compressible gases, the general expression is
V 2 1 V 2 2
h gz q w h gz
2 1 1 2 2 2
For adiabatic flow, q 0; for no external work, w 0; and in most instances changes in
elevation z are very small compared with changes in other parameters and can be neglected.
Then the equation becomes
V 2 1 V 2 2
h h h
2 1 2 2 0
where h is the stagnation enthalpy. The stagnation temperature is then T T V /2c p
2
1
0
0
1
in terms of the temperature and velocity at some point 1. The gas velocity in terms of the
stagnation and static temperatures, respectively, is V 2c (T T ). An increase in ve-
1
0
1
p
locity is accompanied by a decrease in temperature, and vice versa.
For one-dimensional flow of liquids and constant-density (low-velocity) gases, the en-
ergy equation generally is written in terms of energy per unit weight as
V 2 1 p 1 V 2 2 p 2
z w z h
2g 1 2g 2 L
where the first three terms are velocity, pressure, and potential heads, respectively. The head
loss h (u u q)/g and represents the mechanical energy dissipated into thermal
L
1
2
energy irreversibly (the heat transfer q is assumed zero here). It is a positive quantity and
increases in the direction of flow.
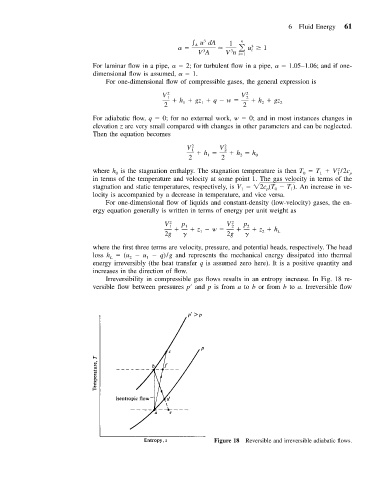
Irreversibility in compressible gas flows results in an entropy increase. In Fig. 18 re-
versible flow between pressures p and p is from a to b or from b to a. Irreversible flow

Figure 18 Reversible and irreversible adiabatic flows.