Page 50 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

1.5 ClassiFiCation oF Vibration 47
If the frequency of the external force coincides with one of the natural frequencies of
the system, a condition known as resonance occurs, and the system undergoes dangerously
large oscillations. Failures of such structures as buildings, bridges, turbines, and airplane
wings have been associated with the occurrence of resonance.

1.5.2 If no energy is lost or dissipated in friction or other resistance during oscillation, the vibra-
undamped tion is known as undamped vibration. If any energy is lost in this way, however, it is called
and damped damped vibration. In many physical systems, the amount of damping is so small that it
can be disregarded for most engineering purposes. However, consideration of damping
Vibration becomes extremely important in analyzing vibratory systems near resonance.

1.5.3 If all the basic components of a vibratory system—the spring, the mass, and the damper—
linear behave linearly, the resulting vibration is known as linear vibration. If, however, any of
and nonlinear the basic components behave nonlinearly, the vibration is called nonlinear vibration. The
differential equations that govern the behavior of linear and nonlinear vibratory systems
Vibration are linear and nonlinear, respectively. If the vibration is linear, the principle of superposi-
tion holds, and the mathematical techniques of analysis are well developed. For nonlinear
vibration, the superposition principle is not valid, and techniques of analysis are less well
known. Since all vibratory systems tend to behave nonlinearly with increasing amplitude
of oscillation, a knowledge of nonlinear vibration is desirable in dealing with practical
vibratory systems.

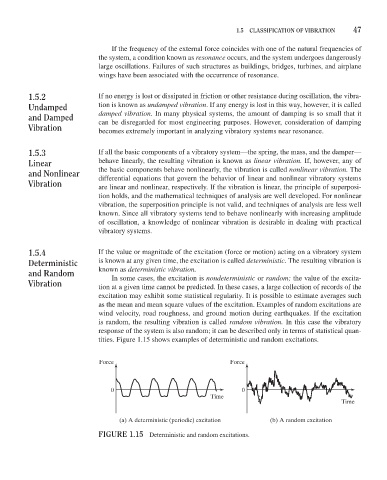
1.5.4 If the value or magnitude of the excitation (force or motion) acting on a vibratory system
deterministic is known at any given time, the excitation is called deterministic. The resulting vibration is
and random known as deterministic vibration.
In some cases, the excitation is nondeterministic or random; the value of the excita-
Vibration tion at a given time cannot be predicted. In these cases, a large collection of records of the
excitation may exhibit some statistical regularity. It is possible to estimate averages such
as the mean and mean square values of the excitation. Examples of random excitations are
wind velocity, road roughness, and ground motion during earthquakes. If the excitation
is random, the resulting vibration is called random vibration. In this case the vibratory
response of the system is also random; it can be described only in terms of statistical quan-
tities. Figure 1.15 shows examples of deterministic and random excitations.

Force Force

0 0
Time
Time

(a) A deterministic (periodic) excitation (b) A random excitation

FiGure 1.15 Deterministic and random excitations.