Page 449 - Mechanics of Asphalt Microstructure and Micromechanics

Multiscale Modeling and Moisture Damage 441

Stress VS Strain under Shearing
0.9
Stress_xy
0.8
0.7
0.6
Stress (GPa) 0.5
0.4
0.3
0.2
0.1
0
0 0.02 0.04 0.06 0.08 0.1
-0.1
Strain
. a S r a e h L n i d a o g
Tensile Loading Stress VS Strain
1
Stress_zz
0.8
0.6
Stress 0.4
0.2
0
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16
-0.2
-0.4
Strain
. b T e l i s n e L g n i d a o
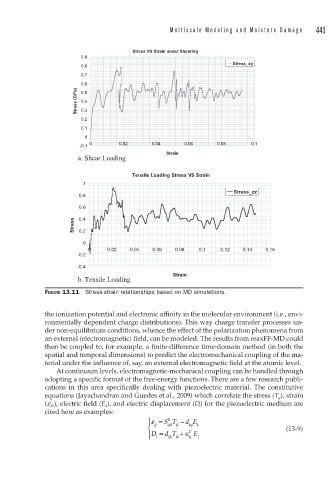
FIGURE 13.11 Stress-strain relationships based on MD simulations.

the ionization potential and electronic affinity in the molecular environment (i.e., envi-
ronmentally dependent charge distributions). This way charge transfer processes un-
der non-equilibrium conditions, whence the effect of the polarization phenomena from
an external (electromagnetic) field, can be modeled. The results from reaxFF-MD could
then be coupled to, for example, a finite-difference time-domain method (in both the
spatial and temporal dimensions) to predict the electromechanical coupling of the ma-
terial under the influence of, say, an external electromagnetic field at the atomic level.
At continuum levels, electromagnetic-mechanical coupling can be handled through
adopting a specific format of the free-energy functions. There are a few research publi-
cations in this area specifically dealing with piezoelectric material. The constitutive
equations (Jayachandran and Guedes et al., 2009) which correlate the stress (T ij ), strain
(e kl ), electric field (E k ), and electric displacement (D i ) for the piezoelectric medium are
cited here as examples:
⎧ ε = ST − d E
E
⎪
⎨ ij ijkl kl kij k (13-9)
⎪ D = d T + ∈ T ij E j
⎩
i
jk
ijk