Page 342 - Microsensors, MEMS and Smart Devices - Gardner Varadhan and Awadelkarim

322 SURFACE ACOUSTIC WAVES IN SOLIDS

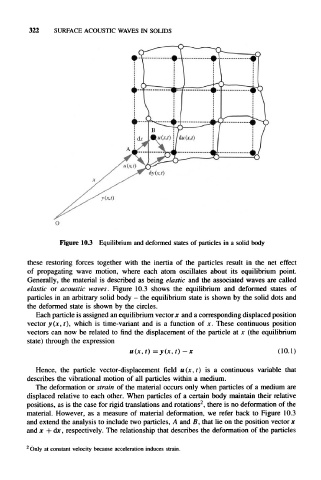
Figure 10.3 Equilibrium and deformed states of particles in a solid body

these restoring forces together with the inertia of the particles result in the net effect
of propagating wave motion, where each atom oscillates about its equilibrium point.
Generally, the material is described as being elastic and the associated waves are called
elastic or acoustic waves. Figure 10.3 shows the equilibrium and deformed states of
particles in an arbitrary solid body - the equilibrium state is shown by the solid dots and
the deformed state is shown by the circles.
Each particle is assigned an equilibrium vector x and a corresponding displaced position
vector y (x, t), which is time-variant and is a function of x. These continuous position
vectors can now be related to find the displacement of the particle at x (the equilibrium
state) through the expression
u(x, t) =y(x, t)— x (10.1)

Hence, the particle vector-displacement field u(x,t) is a continuous variable that
describes the vibrational motion of all particles within a medium.
The deformation or strain of the material occurs only when particles of a medium are
displaced relative to each other. When particles of a certain body maintain their relative
2
positions, as is the case for rigid translations and rotations , there is no deformation of the
material. However, as a measure of material deformation, we refer back to Figure 10.3
and extend the analysis to include two particles, A and B, that lie on the position vector x
and x + dx, respectively. The relationship that describes the deformation of the particles

2
Only at constant velocity because acceleration induces strain.