Page 113 - MODELING OF ASPHALT CONCRETE

Complex Modulus Characterization of Asphalt Concr ete 91

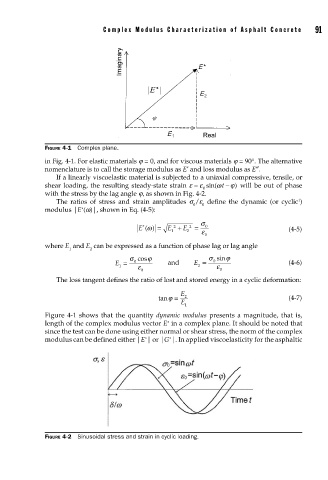
FIGURE 4-1 Complex plane.
in Fig. 4-1. For elastic materials j = 0, and for viscous materials j = 90°. The alternative
nomenclature is to call the storage modulus as E′ and loss modulus as E″.
If a linearly viscoelastic material is subjected to a uniaxial compressive, tensile, or
shear loading, the resulting steady-state strain ε = ε sin( ω − ϕ) will be out of phase
t
0
with the stress by the lag angle j, as shown in Fig. 4-2.
The ratios of stress and strain amplitudes s /e define the dynamic (or cyclic )
1
0
0
∗
modulus |E (w)|, shown in Eq. (4-5):
σ
E () = E + E 2 = 0
ω
*
2
1 2 ε 0 (4-5)
where E and E can be expressed as a function of phase lag or lag angle
1 2
σ cos ϕ σ sin ϕ
E = 0 ε and E = 0 ε (4-6)
2
1
0 0
The loss tangent defines the ratio of lost and stored energy in a cyclic deformation:
tanϕ = E 2 (4-7)
E 1
Figure 4-1 shows that the quantity dynamic modulus presents a magnitude, that is,
∗
length of the complex modulus vector E in a complex plane. It should be noted that
since the test can be done using either normal or shear stress, the norm of the complex
∗
∗
modulus can be defined either |E | or |G |. In applied viscoelasticity for the asphaltic

FIGURE 4-2 Sinusoidal stress and strain in cyclic loading.