Page 114 - MODELING OF ASPHALT CONCRETE

92 Cha pte r F o u r

∗
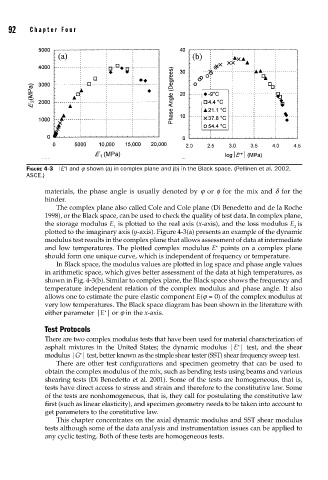
FIGURE 4-3 |E | and j shown (a) in complex plane and (b) in the Black space. (Pellinen et al. 2002,
ASCE.)
materials, the phase angle is usually denoted by j or f for the mix and d for the
binder.
The complex plane also called Cole and Cole plane (Di Benedetto and de la Roche
1998), or the Black space, can be used to check the quality of test data. In complex plane,
the storage modulus E is plotted to the real axis (x-axis), and the loss modulus E is
1 2
plotted to the imaginary axis (y-axis). Figure 4-3(a) presents an example of the dynamic
modulus test results in the complex plane that allows assessment of data at intermediate
∗
and low temperatures. The plotted complex modulus E points on a complex plane
should form one unique curve, which is independent of frequency or temperature.
In Black space, the modulus values are plotted in log space and phase angle values
in arithmetic space, which gives better assessment of the data at high temperatures, as
shown in Fig. 4-3(b). Similar to complex plane, the Black space shows the frequency and
temperature independent relation of the complex modulus and phase angle. It also
allows one to estimate the pure elastic component E(j = 0) of the complex modulus at
very low temperatures. The Black space diagram has been shown in the literature with
∗
either parameter |E | or j in the x-axis.
Test Protocols
There are two complex modulus tests that have been used for material characterization of
∗
asphalt mixtures in the United States; the dynamic modulus |E | test, and the shear
∗
modulus |G | test, better known as the simple shear tester (SST) shear frequency sweep test.
There are other test configurations and specimen geometry that can be used to
obtain the complex modulus of the mix, such as bending tests using beams and various
shearing tests (Di Benedetto et al. 2001). Some of the tests are homogeneous, that is,
tests have direct access to stress and strain and therefore to the constitutive law. Some
of the tests are nonhomogeneous, that is, they call for postulating the constitutive law
first (such as linear elasticity), and specimen geometry needs to be taken into account to
get parameters to the constitutive law.
This chapter concentrates on the axial dynamic modulus and SST shear modulus
tests although some of the data analysis and instrumentation issues can be applied to
any cyclic testing. Both of these tests are homogeneous tests.