Page 226 - Modern Optical Engineering The Design of Optical Systems

Optical Materials 209

reliable through the visible to about 1 m in the near infrared. In his
later work, Herzberger used 0.028 as the denominator constant. The
Conrady equation is empirical and designed for optical glass in the vis-
ible region. All these equations suffer from the drawback that the
index approaches infinity as an absorption wavelength is approached.
Since little use is made of any material close to an absorption band,
this is usually of small consequence.
Until recently Eq. 10.14 was used by Schott and other optical glass
manufacturers as the dispersion equation for optical glass. It is accu-
rate to about 3 10 6 between 0.4 and 0.7 m, and to about 5 10 6
between 0.36 and 1.0 m. The accuracy of Eq. 10.14 can be improved
4
in the ultraviolet by adding a term in , and in the infrared by adding
a term in 10 . More recently, glass manufacturers have switched to
Eq. 10.12, the Sellmeier equation, in order to improve the accuracy.
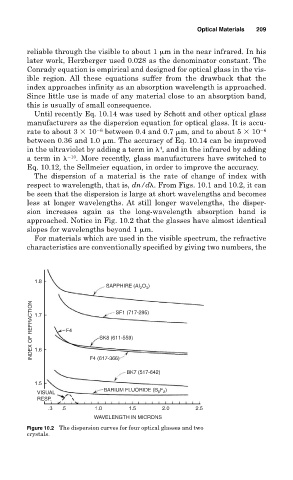
The dispersion of a material is the rate of change of index with
respect to wavelength, that is, dn/d . From Figs. 10.1 and 10.2, it can
be seen that the dispersion is large at short wavelengths and becomes
less at longer wavelengths. At still longer wavelengths, the disper-
sion increases again as the long-wavelength absorption band is
approached. Notice in Fig. 10.2 that the glasses have almost identical
slopes for wavelengths beyond 1 m.
For materials which are used in the visible spectrum, the refractive
characteristics are conventionally specified by giving two numbers, the

1.8
SAPPHIRE (AI O )
2 3
INDEX OF REFRACTION 1.7 F4 SK8 (611-559)
SF1 (717-295)

1.6
F4 (617-366)

BK7 (517-642)
1.5
BARIUM FLUORIDE (B F )
VISUAL 0 2
RESP.
.3 .5 1.0 1.5 2.0 2.5
WAVELENGTH IN MICRONS
Figure 10.2 The dispersion curves for four optical glasses and two
crystals.