Page 42 - Nanotechnology an introduction

realm of physical chemistry and without any specific nanoscale ingredient. A good deal of the phenomenology can be satisfactorily interpreted on
the basis of the Young–Dupré equations (Chapter 3), which allow one to link experimentally accessible single substance surface tensions (e.g., via
contact angle measurements on protein adsorbents (substrata), and on thin films carefully assembled from proteins) to interfacial energies. Wetting
is a typical mesoscale phenomenon with a characteristic length ~30 nm, thus averaging out much molecular detail. This approach has allowed the
systematization of a great deal of data for different proteins adsorbing on different substrata in the presence of different liquid media, rationalizing
the interaction in terms of the interfacial free energy ΔG 123 , the subscripts 1, 2, and 3 denoting adsorbent, liquid medium, and adsorbate
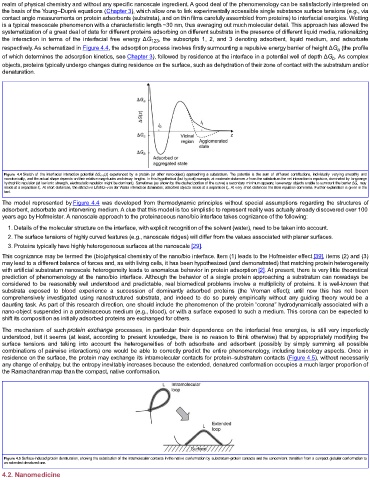
respectively. As schematized in Figure 4.4, the adsorption process involves firstly surmounting a repulsive energy barrier of height ΔG (the profile
a
of which determines the adsorption kinetics, see Chapter 3), followed by residence at the interface in a potential well of depth ΔG . As complex
b
objects, proteins typically undergo changes during residence on the surface, such as dehydration of their zone of contact with the substratum and/or
denaturation.

Figure 4.4 Sketch of the interfacial interaction potential ΔG 123 (z) experienced by a protein (or other nano-object) approaching a substratum. The potential is the sum of different contributions, individually varying smoothly and
monotonically, and the actual shape depends on their relative magnitudes and decay lengths. In this hypothetical (but typical) example, at moderate distances z from the substratum the net interaction is repulsive, dominated by long-range
hydrophilic repulsion (at low ionic strength, electrostatic repulsion might be dominant). Sometimes (as shown by the dashed portion of the curve) a secondary minimum appears; low-energy objects unable to surmount the barrier ΔG a may
reside at a separation ℓ 1 . At short distances, the attractive Lifshitz–van der Waals interaction dominates; adsorbed objects reside at a separation ℓ 0 . At very short distances the Born repulsion dominates. Further explanation is given in the
text.
The model represented by Figure 4.4 was developed from thermodynamic principles without special assumptions regarding the structures of
adsorbent, adsorbate and intervening medium. A clue that this model is too simplistic to represent reality was actually already discovered over 100
years ago by Hofmeister. A nanoscale approach to the proteinaceous nano/bio interface takes cognizance of the following:
1. Details of the molecular structure on the interface, with explicit recognition of the solvent (water), need to be taken into account.
2. The surface tensions of highly curved features (e.g., nanoscale ridges) will differ from the values associated with planar surfaces.
3. Proteins typically have highly heterogeneous surfaces at the nanoscale [29].
This cognizance may be termed the (bio)physical chemistry of the nano/bio interface. Item (1) leads to the Hofmeister effect [39], items (2) and (3)
may lead to a different balance of forces and, as with living cells, it has been hypothesized (and demonstrated) that matching protein heterogeneity
with artificial substratum nanoscale heterogeneity leads to anomalous behavior in protein adsorption [2]. At present, there is very little theoretical
prediction of phenomenology at the nano/bio interface. Although the behavior of a single protein approaching a substratum can nowadays be
considered to be reasonably well understood and predictable, real biomedical problems involve a multiplicity of proteins. It is well-known that
substrata exposed to blood experience a succession of dominantly adsorbed proteins (the Vroman effect); until now this has not been
comprehensively investigated using nanostructured substrata, and indeed to do so purely empirically without any guiding theory would be a
daunting task. As part of this research direction, one should include the phenomenon of the protein “corona” hydrodynamically associated with a
nano-object suspended in a proteinaceous medium (e.g., blood), or with a surface exposed to such a medium. This corona can be expected to
shift its composition as initially adsorbed proteins are exchanged for others.

The mechanism of such protein exchange processes, in particular their dependence on the interfacial free energies, is still very imperfectly
understood, but it seems (at least, according to present knowledge, there is no reason to think otherwise) that by appropriately modifying the
surface tensions and taking into account the heterogeneities of both adsorbate and adsorbent (possibly by simply summing all possible
combinations of pairwise interactions) one would be able to correctly predict the entire phenomenology, including toxicology aspects. Once in
residence on the surface, the protein may exchange its intramolecular contacts for protein–substratum contacts (Figure 4.5), without necessarily
any change of enthalpy, but the entropy inevitably increases because the extended, denatured conformation occupies a much larger proportion of
the Ramachandran map than the compact, native conformation.

Figure 4.5 Surface-induced protein denaturation, showing the substitution of the intramolecular contacts in the native conformation by substratum–protein contacts and the concomitant transition from a compact globular conformation to
an extended denatured one.
4.2. Nanomedicine