Page 298 - Numerical Analysis and Modelling in Geomechanics

ENRICO PRIOLO 279

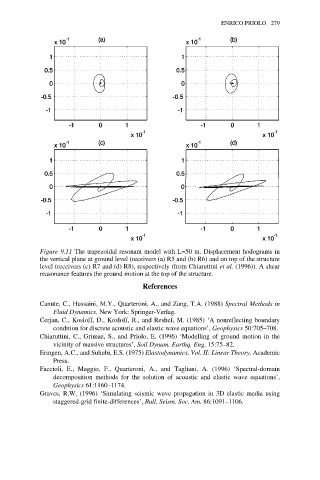
Figure 9.11 The trapezoidal resonant model with L=50 m. Displacement hodograms in
the vertical plane at ground level (receivers (a) R5 and (b) R6) and on top of the structure
level (receivers (c) R7 and (d) R8), respectively (from Chiaruttini et al. (1996)). A shear
reasonance features the ground motion at the top of the structure.
References

Canute, C., Hussaini, M.Y., Quarteroni, A., and Zang, T.A. (1988) Spectral Methods in
Fluid Dynamics, New York: Springer-Verlag.
Cerjan, C., Kosloff, D., Kosloff, R., and Reshef, M. (1985) ‘A nonreflecting boundary
condition for discrete acoustic and elastic wave equations’, Geophysics 50:705–708.
Chiaruttini, C., Grimaz, S., and Priolo, E. (1996) ‘Modelling of ground motion in the
vicinity of massive structures’, Soil Dynam. Earthq. Eng. 15:75–82.
Eringen, A.C., and Suhubi, E.S. (1975) Elastodynamics, Vol. II: Linear Theory, Academic
Press.
Faccioli, E., Maggio, F., Quarteroni, A., and Tagliani, A. (1996) ‘Spectral-domain
decomposition methods for the solution of acoustic and elastic wave equations’,
Geophysics 61:1160–1174.
Graves, R.W. (1996) ‘Simulating seismic wave propagation in 3D elastic media using
staggered-grid finite-differences’, Bull. Seism. Soc. Am. 86:1091–1106.