Page 322 - Numerical Methods for Chemical Engineering

MATLAB summary 311

es wit adative reineent drin stin 2 2
a
1
2 2
1
1 1

1 2
1 2
d
c
2
2
2
1
1 1
2

1 2
1 2

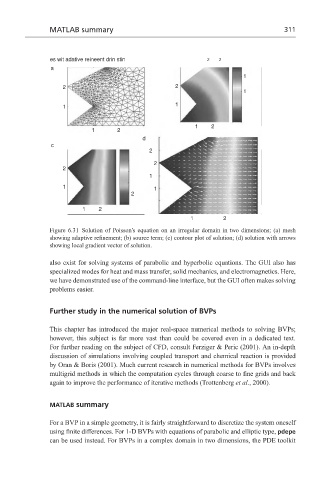
Figure 6.31 Solution of Poisson’s equation on an irregular domain in two dimensions; (a) mesh
showing adaptive refinement; (b) source term; (c) contour plot of solution; (d) solution with arrows
showing local gradient vector of solution.

also exist for solving systems of parabolic and hyperbolic equations. The GUI also has
specialized modes for heat and mass transfer, solid mechanics, and electromagnetics. Here,
we have demonstrated use of the command-line interface, but the GUI often makes solving
problems easier.

Further study in the numerical solution of BVPs

This chapter has introduced the major real-space numerical methods to solving BVPs;
however, this subject is far more vast than could be covered even in a dedicated text.
For further reading on the subject of CFD, consult Ferziger & Peric (2001). An in-depth
discussion of simulations involving coupled transport and chemical reaction is provided
by Oran & Boris (2001). Much current research in numerical methods for BVPs involves
multigrid methods in which the computation cycles through coarse to fine grids and back
again to improve the performance of iterative methods (Trottenberg et al., 2000).

MATLAB summary

For a BVP in a simple geometry, it is fairly straightforward to discretize the system oneself
using finite differences. For 1-D BVPs with equations of parabolic and elliptic type, pdepe
can be used instead. For BVPs in a complex domain in two dimensions, the PDE toolkit