Page 76 - Numerical Methods for Chemical Engineering

Newton’s method for a single equation 65

a 2

1 stin at

1
1 1 2 2

2 at ints
dd 1

1
1 1 2 2

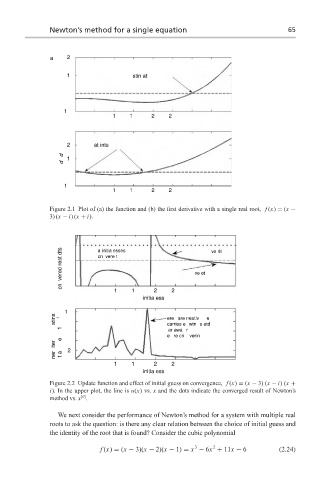
Figure 2.1 Plot of (a) the function and (b) the first derivative with a single real root, f (x) = (x −
3) (x − i)(x + i).

vered rest dts a initia esses ve et ve rit
cn vere t

cn
1 1 2 2
initia ess
1
atins 1 ere are neativ e
carries e wtn s etd
1 ar awa r
e re cn verin
e
ner iter t a 2

1 1 2 2
initia ess

Figure 2.2 Update function and effect of initial guess on convergence, f (x) = (x − 3) (x − i)(x +
i). In the upper plot, the line is u(x) vs. x and the dots indicate the converged result of Newton’s
[0]
method vs. x .
We next consider the performance of Newton’s method for a system with multiple real
roots to ask the question: is there any clear relation between the choice of initial guess and
the identity of the root that is found? Consider the cubic polynomial

3
2
f (x) = (x − 3)(x − 2)(x − 1) = x − 6x + 11x − 6 (2.24)