Page 79 - Numerical Methods for Chemical Engineering

68 2 Nonlinear algebraic systems

initia esses n w cn vere t 2
2
− − 2

2
stin 1 1 initia ess 2
2
2
atins 1 1

1
1
e
ner iter t a

1 1 2 2
initia ess
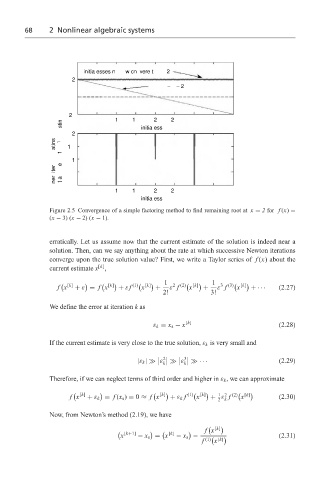
Figure 2.5 Convergence of a simple factoring method to find remaining root at x = 2 for f (x) =
(x − 3) (x − 2) (x − 1).

erratically. Let us assume now that the current estimate of the solution is indeed near a
solution. Then, can we say anything about the rate at which successive Newton iterations
converge upon the true solution value? First, we write a Taylor series of f (x) about the
[k]
current estimate x ,
1 1
[k] [k] (1) [k] 2 (2) [k] 3 (3) [k]
f x + ε = f x + εf x + ε f x + ε f x + ··· (2.27)
2! 3!
We define the error at iteration k as

ε k ≡ x s − x [k] (2.28)

If the current estimate is very close to the true solution, ε k is very small and

|ε k | ε ε ··· (2.29)
2
k k
3
Therefore, if we can neglect terms of third order and higher in ε k , we can approximate
[k] [k] (1) [k] 1 2 (2) [k]
f x + ε k = f (x s ) = 0 ≈ f x + ε k f x + ε f x (2.30)
2 k
Now, from Newton’s method (2.19), we have

[k]
f x
[k+1] [k]
x − x s = x − x s − (2.31)
f (1) x [k]