Page 108 - Numerical methods for chemical engineering

94 2 Nonlinear algebraic systems

a

2
n
1
2

2 2 2 2
a −2 − −2 γ −2 − −2
1 1 a γ
1 1
c d

ω f
2
2 2 2 2
a −2 − −2 γ −2 − −2
1 1 a γ
1 1
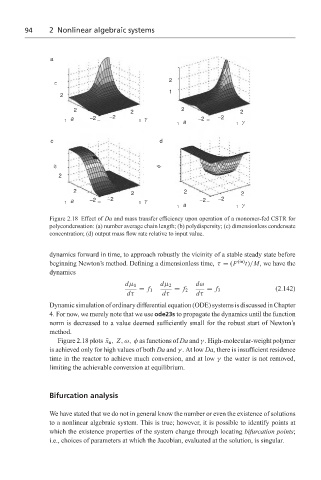
Figure 2.18 Effect of Da and mass transfer efficiency upon operation of a monomer-fed CSTR for
polycondensation: (a) number average chain length; (b) polydispersity; (c) dimensionless condensate
concentration; (d) output mass flow rate relative to input value.

dynamics forward in time, to approach robustly the vicinity of a stable steady state before
beginning Newton’s method. Defining a dimensionless time, τ = (F (in) t)/M,wehavethe
dynamics
dω
dµ 0 dµ 2
= f 1 = f 2 = f 3 (2.142)
dτ dτ dτ
Dynamic simulation of ordinary differential equation (ODE) systems is discussed in Chapter
4. For now, we merely note that we use ode23s to propagate the dynamics until the function
norm is decreased to a value deemed sufficiently small for the robust start of Newton’s
method.
Figure 2.18 plots ¯ x n , Z,ω, φ as functions of Da and γ . High-molecular-weight polymer
is achieved only for high values of both Da and γ .Atlow Da, there is insufficient residence
time in the reactor to achieve much conversion, and at low γ the water is not removed,
limiting the achievable conversion at equilibrium.

Bifurcation analysis

We have stated that we do not in general know the number or even the existence of solutions
to a nonlinear algebraic system. This is true; however, it is possible to identify points at
which the existence properties of the system change through locating bifurcation points;
i.e., choices of parameters at which the Jacobian, evaluated at the solution, is singular.