Page 189 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics

180 The hydrogen atom
z

1

any axis '
z-axis

2
2p z

any axis ' any axis '
x-axis y-axis

2 1 2 1
x y

2p x 2p y

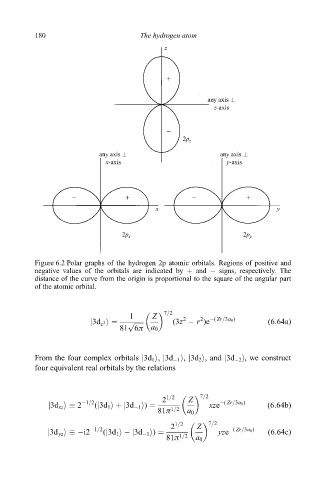
Figure 6.2 Polar graphs of the hydrogen 2p atomic orbitals. Regions of positive and
negative values of the orbitals are indicated by ‡ and ÿ signs, respectively. The
distance of the curve from the origin is proportional to the square of the angular part
of the atomic orbital.

7=2
1 Z 2 2 ÿ( Zr=3a 0 )
j3d 2iˆ p  (3z ÿ r )e (6:64a)
z
81 6ð a 0

From the four complex orbitals j3d 1 i, j3d ÿ1 i, j3d 2 i, and j3d ÿ2 i, we construct
four equivalent real orbitals by the relations

Z
2 1=2 7=2
j3d xz i 2 ÿ1=2 (j3d 1 i‡j3d ÿ1 i) ˆ xze ÿ( Zr=3a 0 ) (6:64b)
81ð 1=2 a 0
Z
2 1=2 7=2
j3d yz i ÿi2 ÿ1=2 (j3d 1 iÿj3d ÿ1 i) ˆ yze ÿ( Zr=3a 0 ) (6:64c)
81ð 1=2 a 0