Page 113 -

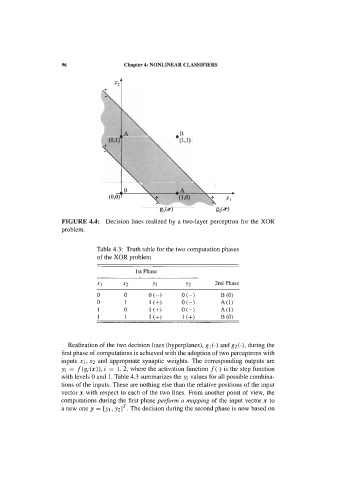
100 4 Statistical Classification

For a two-class discrimination with normal distributions and equal prevalences
and covariance, there is also a simple formula for the probability of error of the
classifier (see e.g. Fukunaga, 1990) :

with:

known as error function5. and

the square of the so-called Bhattacharyya distance, a Mahalanobis distance of the
difference of the means, reflecting the class separability.

Figure 4.19 shows the behaviour of Pe with increasing squared Bhattacharyya
distance. After an initial quick, exponential-like decay, Pe converges
asymptotically to zero. It is, therefore, increasingly difficult to lower a classifier
error when it is already small.
Note that even when the pattern distributions are not normal, as long as they are
symmetric and obey the Mahalanobis metric, we will obtain the same decision
surfaces as for a normal optimum classifier, although with different error rates and
posterior probabilities. As an illustration of this topic, let us consider two classes
with equal prevalences and one-dimensional feature vectors following three
different types of symmetric distributions, with the same unitary standard deviation
and means 0 and 2.3, as shown in Figure 4.20:

(x-m; )2
1 --
Normal distribution: p(x 1 mi) = -e 2"' . (4-26a)
6 s

Cauchy distribution: p(x ( mi) = 11 w [ 1 + [x:mi# -

1 e s
Logistic distribution: p(x I wi) = -
s ( (x-mi) 1' '

5
The error function is the cumulative probability distribution function of N(0,l).