Page 196 - Phase Space Optics Fundamentals and Applications

Imaging Systems: Phase-Space Representations 177

The result in Eq. (5.28) can be readily connected with the ambiguity
function of T( ), as follows. We note that the AF of the pupil mask is
∞

A T ( ,y) = T + T ∗ − exp (i2 y ) d (5.29)
2 2
−∞
2
If we evaluate Eq. (5.29) at y = [2 /( )]W 2,0 , then

2W 2,0
A T , =|H( ,W 2,0 )| (5.30)

2
In other words, if one evaluates the modulus of the AF, |A T ( ,y)|,
along the straight line y = m , then one obtains the MTF |H( ,W 2,0 )|
2
with focus error coefficient W 2,0 = ( /2)m . Hence, we recognize
that |A T ( ,y)| contains all the possible MTFs |H( ; W 2,0 )| for variable
focus error W 2,0 . See Ref. 19.
Next we note that the simple result in Eq. (5.30) has the two fol-
lowing applications. First, one can visualize (in a single picture) the
impact of variable focus error on the MTF. Second, one can seek pupil
masks that generated rotationally symmetric AF, for reducing the in-
fluence of focus error on the MTF. And in this manner, one can extend
the depth of field of an optical system.
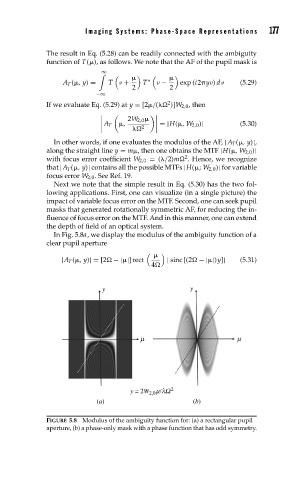
In Fig. 5.8a, we display the modulus of the ambiguity function of a
clear pupil aperture

|A T ( ,y)|= [2 −| |] rect | sinc [(2 −| |)y]| (5.31)
4

y y

m m

y =2W 2,0 m/lW 2
(a) (b)

FIGURE 5.8 Modulus of the ambiguity function for: (a) a rectangular pupil
aperture, (b) a phase-only mask with a phase function that has odd symmetry.