Page 154 - Physical Principles of Sedimentary Basin Analysis

136 Heat flow

t = 0.001
1.0

0.8 t = 0.08 t = 0.04 t = 0.02

0.6
T [−]
^
t = 0.16
0.4

0.2
t=infinity
0.0
0.0 0.2 0.4 0.6 0.8 1.0
^ r [−]
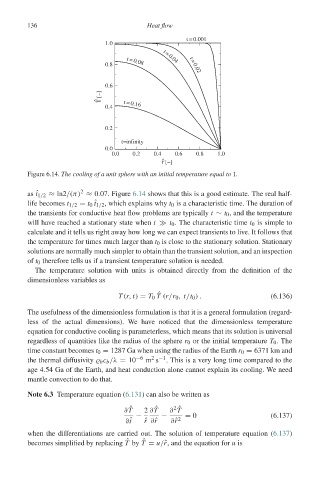
Figure 6.14. The cooling of a unit sphere with an initial temperature equal to 1.

2
as ˆ t 1/2 ≈ ln2/(π) ≈ 0.07. Figure 6.14 shows that this is a good estimate. The real half-
life becomes t 1/2 = t 0 t 1/2 , which explains why t 0 is a characteristic time. The duration of
ˆ
the transients for conductive heat flow problems are typically t ∼ t 0 , and the temperature
will have reached a stationary state when t
t 0 . The characteristic time t 0 is simple to
calculate and it tells us right away how long we can expect transients to live. It follows that
the temperature for times much larger than t 0 is close to the stationary solution. Stationary
solutions are normally much simpler to obtain than the transient solution, and an inspection
of t 0 therefore tells us if a transient temperature solution is needed.
The temperature solution with units is obtained directly from the definition of the
dimensionless variables as

ˆ
T (r, t) = T 0 T (r/r 0 , t/t 0 ) . (6.136)
The usefulness of the dimensionless formulation is that it is a general formulation (regard-
less of the actual dimensions). We have noticed that the dimensionless temperature
equation for conductive cooling is parameterless, which means that its solution is universal
regardless of quantities like the radius of the sphere r 0 or the initial temperature T 0 .The
time constant becomes t 0 = 1287 Ga when using the radius of the Earth r 0 = 6371 km and
2 −1
the thermal diffusivity b c b /λ = 10 −6 m s . This is a very long time compared to the
age 4.54 Ga of the Earth, and heat conduction alone cannot explain its cooling. We need
mantle convection to do that.

Note 6.3 Temperature equation (6.131) can also be written as
∂T ˆ 2 ∂T ˆ ∂ T
2 ˆ
− − = 0 (6.137)
∂ ˆ t ˆ r ∂ ˆ r ∂ ˆ r 2
when the differentiations are carried out. The solution of temperature equation (6.137)
becomes simplified by replacing T by T = u/ˆ, and the equation for u is
r
ˆ
ˆ