Page 22 - Physical Principles of Sedimentary Basin Analysis

4 Properties of porous media

bi
Pores
qz
mu
200 μm
Grains
(a) (b)
Figure 2.1. (a) A regular porous medium made of grains of equal size. (b) A SEM image of a sandstone
where the pore space is black and the quartz grains are gray. (qz = quartz, mu = muscovite and
bi = biotite)

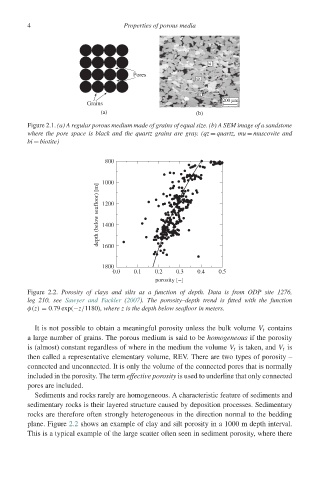
800

1000
depth (below seafloor) [m] 1200

1400

1600

1800
0.0 0.1 0.2 0.3 0.4 0.5
porosity [−]
Figure 2.2. Porosity of clays and silts as a function of depth. Data is from ODP site 1276,
leg 210, see Sawyer and Fackler (2007). The porosity–depth trend is fitted with the function
φ(z) = 0.79 exp(−z/1180), where z is the depth below seafloor in meters.

It is not possible to obtain a meaningful porosity unless the bulk volume V t contains
a large number of grains. The porous medium is said to be homogeneous if the porosity
is (almost) constant regardless of where in the medium the volume V t is taken, and V t is
then called a representative elementary volume, REV. There are two types of porosity –
connected and unconnected. It is only the volume of the connected pores that is normally
included in the porosity. The term effective porosity is used to underline that only connected
pores are included.
Sediments and rocks rarely are homogeneous. A characteristic feature of sediments and
sedimentary rocks is their layered structure caused by deposition processes. Sedimentary
rocks are therefore often strongly heterogeneous in the direction normal to the bedding
plane. Figure 2.2 shows an example of clay and silt porosity in a 1000 m depth interval.
This is a typical example of the large scatter often seen in sediment porosity, where there