Page 220 - Physical Principles of Sedimentary Basin Analysis

202 Subsidence

0.0

0.1

s/c [−] 0.2

0.3

0.4
1 2 3 4 5
β [−]
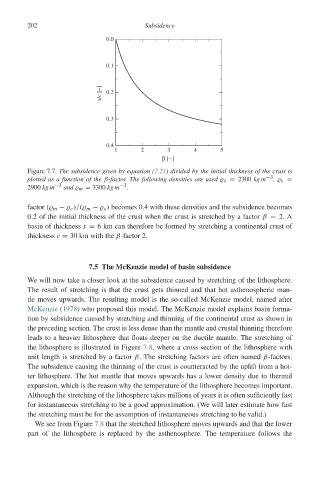
Figure 7.7. The subsidence given by equation (7.21) divided by the initial thickness of the crust is
plotted as a function of the β-factor. The following densities are used s = 2300 kg m −3 , c =
2900 kg m −3 and m = 3300 kg m −3 .

factor ( m − c )/( m − s ) becomes 0.4 with these densities and the subsidence becomes
0.2 of the initial thickness of the crust when the crust is stretched by a factor β = 2. A
basin of thickness s = 6 km can therefore be formed by stretching a continental crust of
thickness c = 30 km with the β-factor 2.

7.5 The McKenzie model of basin subsidence
We will now take a closer look at the subsidence caused by stretching of the lithosphere.
The result of stretching is that the crust gets thinned and that hot asthenospheric man-
tle moves upwards. The resulting model is the so-called McKenzie model, named after
McKenzie (1978) who proposed this model. The McKenzie model explains basin forma-
tion by subsidence caused by stretching and thinning of the continental crust as shown in
the preceding section. The crust is less dense than the mantle and crustal thinning therefore
leads to a heavier lithosphere that floats deeper on the ductile mantle. The stretching of
the lithosphere is illustrated in Figure 7.8, where a cross-section of the lithosphere with
unit length is stretched by a factor β. The stretching factors are often named β-factors.
The subsidence causing the thinning of the crust is counteracted by the uplift from a hot-
ter lithosphere. The hot mantle that moves upwards has a lower density due to thermal
expansion, which is the reason why the temperature of the lithosphere becomes important.
Although the stretching of the lithosphere takes millions of years it is often sufficiently fast
for instantaneous stretching to be a good approximation. (We will later estimate how fast
the stretching must be for the assumption of instantaneous stretching to be valid.)
We see from Figure 7.8 that the stretched lithosphere moves upwards and that the lower
part of the lithosphere is replaced by the asthenosphere. The temperature follows the