Page 227 - Physical Principles of Sedimentary Basin Analysis

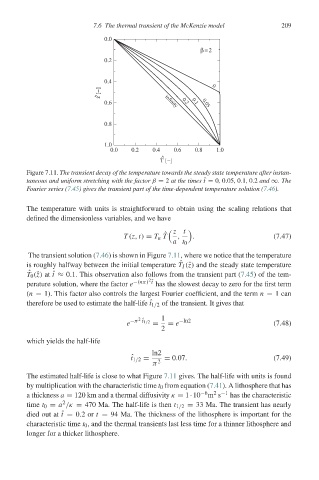
7.6 The thermal transient of the McKenzie model 209

0.0
β = 2
0.2

0.4 0
z [−]
^
0.6 infinity 0.2 0.1 0.05

0.8

1.0
0.0 0.2 0.4 0.6 0.8 1.0
^
T [−]
Figure 7.11. The transient decay of the temperature towards the steady state temperature after instan-
taneous and uniform stretching with the factor β = 2 at the times ˆ t = 0, 0.05, 0.1, 0.2 and ∞.The
Fourier series (7.45) gives the transient part of the time-dependent temperature solution (7.46).

The temperature with units is straightforward to obtain using the scaling relations that
defined the dimensionless variables, and we have
z t

T (z, t) = T a T ˆ , . (7.47)
a t 0
The transient solution (7.46) is shown in Figure 7.11, where we notice that the temperature
ˆ
is roughly halfway between the initial temperature T I (ˆz) and the steady state temperature
T 0 (ˆz) at ˆ t ≈ 0.1. This observation also follows from the transient part (7.45)ofthetem-
ˆ
2
perature solution, where the factor e −(nπ) ˆ t has the slowest decay to zero for the first term
(n = 1). This factor also controls the largest Fourier coefficient, and the term n = 1 can
therefore be used to estimate the half-life ˆ t 1/2 of the transient. It gives that
2 1 −ln2
e −π ˆ t 1/2 = = e (7.48)
2
which yields the half-life
ln2
ˆ t 1/2 = = 0.07. (7.49)
π 2
The estimated half-life is close to what Figure 7.11 gives. The half-life with units is found
by multiplication with the characteristic time t 0 from equation (7.41). A lithosphere that has
2 −1
a thickness a = 120 km and a thermal diffusivity κ = 1·10 −6 m s has the characteristic
2
time t 0 = a /κ = 470 Ma. The half-life is then t 1/2 = 33 Ma. The transient has nearly
died out at ˆ t = 0.2or t = 94 Ma. The thickness of the lithosphere is important for the
characteristic time t 0 , and the thermal transients last less time for a thinner lithosphere and
longer for a thicker lithosphere.