Page 74 - Physical chemistry eng

3.2 THE DEPENDENCE OF U ON V AND T 51

determined as a function of T as discussed in Section 2.5, the following integral is
numerically evaluated:

T 2 T 2
¢U = C dT = n C V, m dT (3.16)
V
V
3 3
T 1 T 1
Over a limited temperature range, C V, m can often be regarded as a constant. If this is
the case, Equation (3.16) simplifies to

T 2
¢U = C dT = C ¢T = nC V, m ¢T (3.17)
V
V
V
3
T 1
which can be written in a different form to explicitly relate q and ¢U :
V
f f
0U
dq = a b dT or q =¢U (3.18)
V
V
0T V
3 3
i i
Although dq is not an exact differential, the integral has a unique value if the path
is defined, as it is in this case (constant volume). Equation (3.18) shows that ¢U
for an arbitrary process in a closed system in which only P–V work occurs can be
determined by measuring q under constant volume conditions. As discussed in
Chapter 4, the technique of bomb calorimetry uses this approach to determine ¢U
for chemical reactions.
Next consider the dependence of U on V at constant T, or (0U>0V) T . This quantity
2
2
-2
has the units of J>m = (J>m)>m = kgms >m = force>area = pressure and is
3
called the internal pressure. To explicitly evaluate the internal pressure for different
substances, a result will be used that is derived in the discussion of the second law of
thermodynamics in Section 5.12:
0U 0P
a b = Ta b - P (3.19)
0V T 0T V
Using this equation, the total differential of the internal energy can be written as

0P
dU = dU + dU = C dT + BTa b - PRdV (3.20)
V
T
V
0T V V ,T f V ,T f
f
i
In this equation, the symbols dU and dU have been used, where the subscript indi-
V
T
cates which variable is constant. Equation (3.20) is an important result that applies to
systems containing gases, liquids, or solids in a single phase (or mixed phases at a con-
stant composition) if no chemical reactions or phase changes occur. The advantage of
writing dU in the form given by Equation (3.20) over that in Equation (3.12) is that
(0U>0V) T can be evaluated in terms of the system variables P, V, and T and their deriv- T
atives, all of which are experimentally accessible.
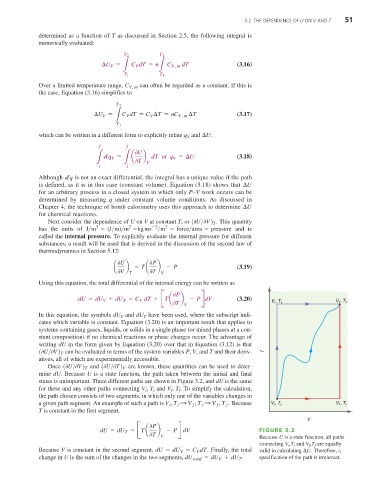
Once (0U>0V) T and (0U>0T) V are known, these quantities can be used to deter-
mine dU. Because U is a state function, the path taken between the initial and final
states is unimportant. Three different paths are shown in Figure 3.2, and dU is the same
for these and any other paths connecting V , T and V , T . To simplify the calculation,
f
f
i
i
the path chosen consists of two segments, in which only one of the variables changes in
a given path segment. An example of such a path is V , T : V , T : V , T f . Because V ,T i V ,T i
f
i
i
f
f
i
i
T is constant in the first segment,
V
0P
dU = dU = BTa b - PR dV FIGURE 3.2
T
0T V Because U is a state function, all paths
connecting V i ,T i and V f ,T f are equally
Because V is constant in the second segment, dU = dU = C dT . Finally, the total valid in calculating ¢U . Therefore, a
V
V
change in U is the sum of the changes in the two segments, dU total = dU + dU T . specification of the path is irrelevant.
V