Page 46 - Physical Chemistry

lev38627_ch01.qxd 2/20/08 11:38 AM Page 27

27
Section 1.8
Integral Calculus

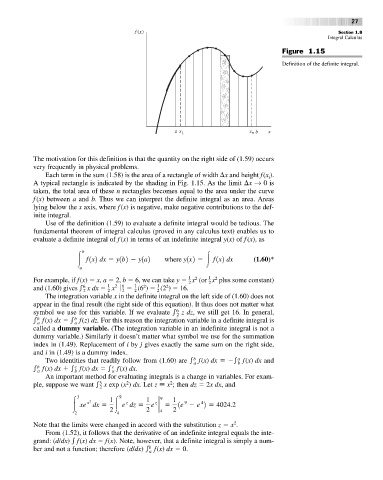
Figure 1.15
Definition of the definite integral.

The motivation for this definition is that the quantity on the right side of (1.59) occurs
very frequently in physical problems.
Each term in the sum (1.58) is the area of a rectangle of width x and height f(x ).
i
A typical rectangle is indicated by the shading in Fig. 1.15. As the limit x → 0is
taken, the total area of these n rectangles becomes equal to the area under the curve
f (x) between a and b. Thus we can interpret the definite integral as an area. Areas
lying below the x axis, where f(x)isnegative, make negative contributions to the def-
inite integral.
Use of the definition (1.59) to evaluate a definite integral would be tedious. The
fundamental theorem of integral calculus (proved in any calculus text) enables us to
evaluate a definite integral of f (x) in terms of an indefinite integral y(x) of f(x), as
b
f 1x2 dx y1b2 y1a2 where y1x2 f 1x2 dx (1.60)*

a
1
1
2
2
For example, if f(x) x, a 2, b 6, we can take y x (or x plus some constant)
2
2
1
1
and (1.60) gives xdx x ƒ 1 2 (6 ) (2 ) 16.
6
6
2
2
2
2
2
2
2
The integration variable x in the definite integral on the left side of (1.60) does not
appear in the final result (the right side of this equation). It thus does not matter what
6
symbol we use for this variable. If we evaluate zdz, we still get 16. In general,
2
b
b
f(x) dx f(z) dz. For this reason the integration variable in a definite integral is
a
a
called a dummy variable. (The integration variable in an indefinite integral is not a
dummy variable.) Similarly it doesn’t matter what symbol we use for the summation
index in (1.49). Replacement of i by j gives exactly the same sum on the right side,
and i in (1.49) is a dummy index.
b
a
Two identities that readily follow from (1.60) are f(x) dx f(x) dx and
b
a
b
c
c
f(x) dx f(x) dx f(x) dx.
b
a
a
An important method for evaluating integrals is a change in variables. For exam-
2
3
2
ple, suppose we want x exp (x ) dx. Let z x ; then dz 2xdx, and
2
3 xe dx 1 9 e dz 1 e ` 1 1e e 2 4024.2
9
2
x
9
z
z
4
2 2 4 2 4 2
2
Note that the limits were changed in accord with the substitution z x .
From (1.52), it follows that the derivative of an indefinite integral equals the inte-
grand: (d/dx) f(x) dx f(x). Note, however, that a definite integral is simply a num-
b
ber and not a function; therefore (d/dx) f(x) dx 0.
a