Page 74 - Physical Chemistry

lev38627_ch02.qxd 2/29/08 3:11 PM Page 55

55
where the P subscripts indicate that the infinitesimal changes dU, dT, and dV occur at Section 2.7
The Joule and
constant P. Division by dT gives Joule–Thomson Experiments
P
dU P 0U 0U dV P
a b a b
dT P 0T V 0V T dT P

The ratio of infinitesimals dU /dT is the partial derivative ( U/ T) , so
P
P
P
0U 0U 0U 0V
a b a b a b a b (2.60)
0T P 0T V 0V T 0T P
Substitution of (2.60) into (2.57) gives the desired relation:

0U 0V
C C ca b Pda b (2.61)
V
P
0V T 0T P
The state function ( U/ V) in (2.61) has dimensions of pressure and is some-
T
times called the internal pressure. Clearly, ( U/ V) is related to that part of the
T
internal energy U that is due to intermolecular potential energy. A change in the sys-
tem’s volume V will change the average intermolecular distance and hence the aver-
age intermolecular potential energy. For gases not at high pressure, the smallness of
intermolecular forces makes ( U/ V) in (2.61) small. For liquids and solids, where
T
molecules are close to one another, the large intermolecular forces make ( U/ V) T
large. Measurement of ( U/ V) in gases is discussed in Sec. 2.7.
T

2.7 THE JOULE AND JOULE–THOMSON EXPERIMENTS
In 1843 Joule tried to determine ( U/ V) for a gas by measuring the temperature
T
change after free expansion of the gas into a vacuum. This experiment was repeated
by Keyes and Sears in 1924 with an improved setup (Fig. 2.6).
Initially, chamber A is filled with a gas, and chamber B is evacuated. The valve
between the chambers is then opened. After equilibrium is reached, the temperature
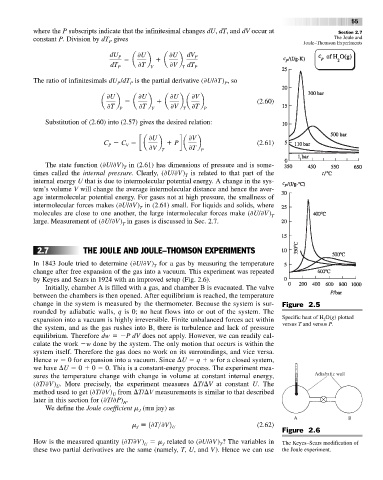
change in the system is measured by the thermometer. Because the system is sur- Figure 2.5
rounded by adiabatic walls, q is 0; no heat flows into or out of the system. The
expansion into a vacuum is highly irreversible. Finite unbalanced forces act within Specific heat of H O(g) plotted
2
versus T and versus P.
the system, and as the gas rushes into B, there is turbulence and lack of pressure
equilibrium. Therefore dw PdV does not apply. However, we can readily cal-
culate the work w done by the system. The only motion that occurs is within the
system itself. Therefore the gas does no work on its surroundings, and vice versa.
Hence w 0 for expansion into a vacuum. Since U q w for a closed system,
we have U 0 0 0. This is a constant-energy process. The experiment mea-
sures the temperature change with change in volume at constant internal energy,
( T/ V) . More precisely, the experiment measures T/ V at constant U. The
U
method used to get ( T/ V) from T/ V measurements is similar to that described
U
later in this section for ( T/ P) .
H
We define the Joule coefficient m (mu jay) as
J
m 10T>0V2 U (2.62)
J
Figure 2.6
How is the measured quantity ( T/ V) m related to ( U/ V) ? The variables in The Keyes–Sears modification of
U
J
T
these two partial derivatives are the same (namely, T, U, and V). Hence we can use the Joule experiment.