Page 85 - Pipelines and Risers

58 Chapter 3

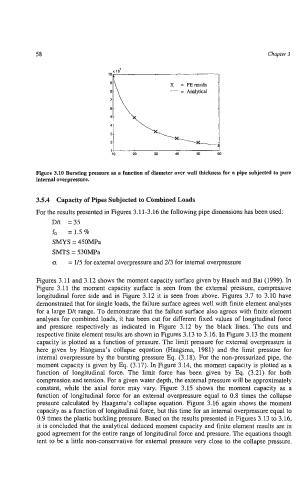
x =FEresutts .
=
- Analytical -

2-
3
1
10 20 30 40 50 60
Figure 3.10 Bursting pressure as a function of diameter over wall thickness for a pipe subjected to pure
internal overpressure.

3.5.4 Capacity of Pipes Subjected to Combined Loads
For the results presented in Figures 3.11-3.16 the following pipe dimensions has been used
Dlt = 35
fo = 1.5 %
SMYS = 450MPa
SMTS = 530MPa
a = 1/5 for external overpressure and 2/3 for internal overpressure

Figures 3.11 and 3.12 shows the moment capacity surface given by Hauch and Bai (1999). In
Figure 3.11 the moment capacity surface is seen from the external pressure, compressive
longitudinal force side and in Figure 3.12 it is seen from above. Figures 3.7 to 3.10 have
demonstrated that for single loads, the failure surface agrees well with finite element analyses
for a large D/t range. To demonstrate that the failure surface also agrees with finite element
analyses for combined loads, it has been cut for different fixed values of longitudinal force
and pressure respectively as indicated in Figure 3.12 by the black lines. The cuts and
respective finite element results are shown in Figures 3.13 to 3.16. In Figure 3.13 the moment
capacity is plotted as a function of pressure. The limit pressure for external overpressure is
here given by Haagsma’s collapse equation (Haagsma, 1981) and the limit pressure for
internal overpressure by the bursting pressure Eq. (3.18). For the non-pressurized pipe, the
moment capacity is given by Eq. (3.17). In Figure 3.14, the moment capacity is plotted as a
function of longitudinal force. The limit force has been given by Eq. (3.21) for both
compression and tension. For a given water depth, the external pressure will be approximately
constant, while the axial force may vary. Figure 3.15 shows the moment capacity as a
function of longitudinal force for an external Overpressure equal to 0.8 times the collapse
pressure calculated by Haagsma’s collapse equation. Figure 3.16 again shows the moment
capacity as a function of longitudinal force, but this time for an internal overpressure equal to
0.9 times the plastic buckling pressure. Based on the results presented in Figures 3.13 to 3.16,
it is concluded that the analytical deduced moment capacity and finite element results are in
good agreement for the entire range of longitudinal force and pressure. The equations though
tent to be a little non-conservative for external pressure very close to the collapse pressure.