Page 142 - Plastics Engineering

Mechanical Behaviour of Plastics 125

1 2 3 4 5 6
a (mm)
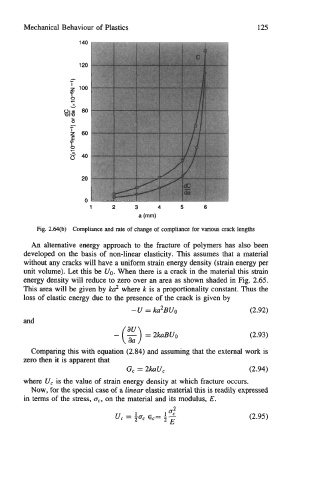
Fig. 2.w) Compliance and rate. of change of compliance for various crack lengths

An alternative energy approach to the fracture of polymers has also been
developed on the basis of non-linear elasticity. This assumes that a material
without any cracks will have a uniform strain energy density (strain energy per
unit volume). Let this be UO. When there is a crack in the material this strain
energy density will reduce to zero over an area as shown shaded in Fig. 2.65.
This area will be given by &a2 where k is a proportionality constant. Thus the
loss of elastic energy due to the presence of the crack is given by
-U = &a2BUo (2.92)
and
(2.93)

Comparing this with equation (2.84) and assuming that the external work is
zero then it is apparent that
G, = 2hU, (2.94)
where U, is the value of strain energy density at which fracture occurs.
Now, for the special case of a linear elastic material this is readily expressed
in terms of the stress, a,, on the material and its modulus, E.

(2.95)