Page 220 - Plastics Engineering

Mechanical Behaviour of Composites 203
layer. At first glance it might appear that the best means of achieving a more
isotropic behaviour would be to have two layers with the unidirectional fibres
arranged perpendicular to each other. For example, two layers arranged at 0"
and 90" to the global x-direction or at +45" and -45" to the x-direction might
appear to offer more balanced properties in all directions. In fact the lack of
symmetry about the centre plane of the laminate causes very complex behaviour
in such cases.
In general it is best to aim for symmetry about the centre plane. A lami-
nate in which the layers above the centre plane are a mirror image of those
below it is described as symmetric. Thus a four stack laminate with fibres
oriented at 0", 90", 90" and 0" is symmetric. The convention is to denote this
as [oo/900/900/o"]T or [0", 90;, Oo]T or [0"/90"],. In general terms any laminate
of the type [e, -8, -8, e]T is symmetric and there may of course be any even
number of layers or plies. They do not all have to be the same thickness but
symmetry must be maintained. In the case of a symmetric laminate where the
central ply is not repeated, this can be denoted by the use of an overbar. Thus
the laminate [45/ - 45/0/90/0/ - 45/45]T can be written as [f45,0, %lS.

In-plane Behaviour of a Symmetric Laminate
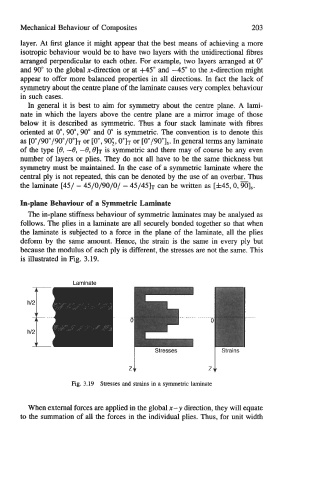
The in-plane stiffness behaviour of symmetric laminates may be analysed as
follows. The plies in a laminate are all securely bonded together so that when
the laminate is subjected to a force in the plane of the laminate, all the plies
deform by the same amount. Hence, the strain is the same in every ply but
because the modulus of each ply is different, the stresses are not the same. This
is illustrated in Fig. 3.19.

Fig. 3.19 Stresses and strains in a symmetric laminate

When external forces are applied in the global x-y direction, they will equate
to the summation of all the forces in the individual plies. Thus, for unit width