Page 220 - Practical Ship Design

184 Chapter 6

I .4

Assumes:
1. Normal stern lines
2. Fairly full C,
1.3 3. LCB match to C, to
normal practice
4. T/L = 0.06
(1 =K)

1.2

I .l

1 .o
0.4 0.5 0.6 0.7 0.8 0.9
Cb

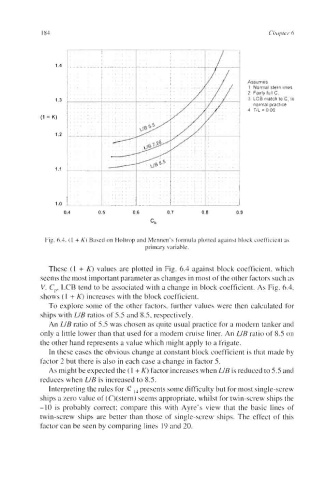
Fig. 6.4. (1 + K) Based on Holtrop and Mennen’s formula plotted against block coefficient as
primary variable.

These (1 + K) values are plotted in Fig. 6.4 against block coefficient, which
seems the most important parameter as changes in most of the other factors such as
V, Cp, LCB tend to be associated with a change in block coefficient. As Fig. 6.4,
shows (1 + K) increases with the block coefficient.
To explore some of the other factors, further values were then calculated for
ships with LIB ratios of 5.5 and 8.5, respectively.
An LIB ratio of 5.5 was chosen as quite usual practice for a modern tanker and
only a little lower than that used for a modern cruise liner. An LIB ratio of 8.5 on
the other hand represents a value which might apply to a frigate.
In these cases the obvious change at constant block coefficient is that made by
factor 2 but there is also in each case a change in factor 5.
As might be expected the (1 + K) factor increases when LIB is reduced to 5.5 and
reduces when LIB is increased to 8.5.
Interpreting the rules for @Il4 presents some difficulty but for most single-screw
ships a zero value of (C)(stern) seems appropriate, whilst for twin-screw ships the
-10 is probably correct; compare this with Ayre’s view that the basic lines of
twin-screw ships are better than those of single-screw ships. The effect of this
factor can be seen by comparing lines 19 and 20.