Page 185 - Pressure Swing Adsorption

PRESSURE SWING ADSORPTION EQUILIBRIUM THEORY 161
160
and blowctown [Figure 4.24(b)], over identical pressure ratios, calculated by the effect of '3 nonlinear isotherm and the effect of usm:g the Ergun equation
numerical integration of Ea. 4.77. 36 Blowctown is clearly slower than oressur- for pressure drop (in place of Darcy's Law) have been mvesttgated by
-
izat10n. The dimensionless times for pressunzatton and blowdown are, re- Rodrigues et al. 33 36
soecllvely, about three and ten times the charactenst1c time defined by: One situation of special interest 1s to use a PSA process to conc.entrate
strongly adsorbed comoonent(s) from a feed of low concentration. An exam-
36
ple of this was studied by Rodrigues et al. The bed is 1hitially at eauilibnum
(4.81)
with a linearly adsorbed light component, at mole frattIOn 0.5 and a total
pressure of 5.0 atm. As the bed is deoressunzect to atmosohenc pressure, the
In this example, the pressure profiles during pressunzatton and blow~own pressure along the axis of the bed responds as shown m Figure 4.25(a).
both assume the form of simple propagating waves. With mixtures of drffer- Simultaneously, as shown in Figure 4.25(b), the mole fraction of the more
ently adsorbed components (or with mrxtures of inert and_ adsorbing spec1~s) strongly adsorbed component r1ses rapidly at the open end of the bed, to
the profiles assume more comolex forms. Many such ram1ficat1ons, mcludmg about 0.65, and the profile then pivots about this point until it reaches a more
or less uniform profile through the bed. Thereafter, the profile remains
almost uniform through the bed, rising asymptotically towards YA ::::: 0.90. At
this ooint 1 essentially aII the less strongly adsorbed species have been re-
s I moved from the bed, and 1t would be possible, in principle, to recover the
I strongly adsorbed species m highly concentrated form by deep evacuation of
l
3., 1 the bed (see Sect10n 6.10 ).
t, t, An alternative approach has been followed by Scott, 38 who has shown
that, if the column can be regarded as mfimtely iong, a relatively s1mole
4
analytical solutwn may be obtamed. Profiles of oressure and composition for
oressunzation and blowdown, calculated with parameters reoresentat1ve of
air-zeolite SA, are shown ill Figure 4.26. The composition profiles for
pressurization fFigure 4.26(a)J show a complex wave form that includes a
A
3 partial shock, which appears as an inflection at small values of 0. The orofiles
for blowdown [Figure 4.26(b)l contam only s1mole waves; that is, they are
~ I everywhere concave downwards.
~
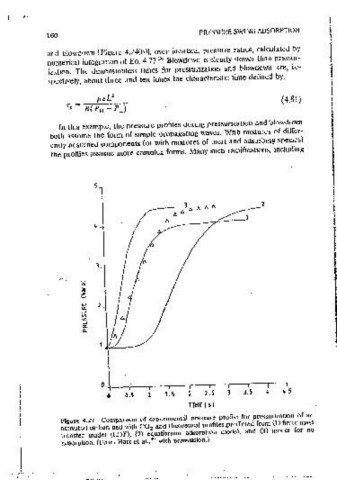
-" ;.I I The effect of finite mass transfer rate has been mvestigated by Hart et al. 39
w 2 , I Their exoenmental data for oressunzat10n of an activated carbon bed with
0:
::, I CO are shown m Figure 4.27 together with theoretical curves calculated
~ 2
~
w according to tht"ee different assumptions: negligible adsorption, instanta-
0:
n. neous adsorption, and adsorptton at a fimte rate according to the linear
dnv1ng force (LDF) model (k - 0.2 s- '). The expenmental data lie closest to
i
the fimte rate model, although there is a significant devrnt1on in the long-time
region. It seems likely that this dev1at1on may be attributed to heat effects,
which will reduce adsorption m the long-time region.
o L-,--.--,--.---,--.---r-,----,
0 o., 1 LS 2 2,5 3 3.5 ,.5
TJHE Isl 4.10 Conclusions
Fig r 4 27 Companson of expertmental _pressure profile for pressunzatmn of an The iocal equilibnum theory approach 1s the s1rnolest available for s1mulatmg
act::a~eci carbon bed with CO and theoretical profiles _predicted.from (1) fimte mass or designing PSA systems. Furthermore, when ctata are soarse (e.g., no PSA
2
transfer model (LDF), (2) equilibrium adsorption model, and (3) model for no
adsorption. (From Hart et al., 39 with oerrn1ssionJ pilot plant data), it is the most reliable method because It does not depend