Page 182 - Pressure Swing Adsorption

156 PRESSURE SWING ADSORPTION EQUILIBRIUM THEORY 157

taking mto account pressure gradients through the column, has attracted
much attention recently. For example, a detailed moctei was suggested by 6 1 e
33 35 p ~
Lu et ai., ~ who studied both pressunzat10n and blowdown. Their model
included mass transfer resistances, axial dispersion, mtraparticle convection, (atm) 5 2 3
and axial pressure drop, but not heat effects, and was solved by finite l.5
6 41
differences. Other similar models have been suggested,3 - and a brief 4
summary of the major conclusions from that work 1s given here. 1-----,
To a first approx1mat10n, the oressure droo through a packed adsorbent
bed can be represented by Darcy's Law: 3
-B ap
v= --- ( 4.76)
µ. oz 2
Couoling this with the differential fluid phase mass balance for a plug flow
system (cf. Eo. 5.2) with raoid equilibration yields 1

ap[ = B a [P(aP)] ( 4.77) 0
at , µ[e + (1 - e)(dq* /de)] az az , , l 0.0 0.2 0.4 0.6 0.8 X 1.0

where, for an isothermal system, da* / de reoresents simply the local slope of (a)
the equilibnum isotherm. The appropnate initial and boundary conditions
are, for pressunzation: I 6

t = 0, for all z ( 4.78) p
t > 0, for z = 0 (atm) 5

4

with Pu and PL mterchanged for blowdown.
When pressure ctrop through the column is negligible, Eo. 4.77 is eomva- 3
lent to EQ. 4.6, which was discussed previously. For a pure gas, A, tt reduces
to:
2 2
3
( 4.79) 5
1 l e,
10
wherf:: the .sign reflects the onentatmn of the column and the direction of
flow. This may be mtegrated directly to obtam the dimensionless time o.
required to oressunze or depressurize the bed:
0.0 0.2 0.4 0.6 0.8 1.0
X
~ = volume of gas feel to the column = In ffJ
- holdup m the column ( 4.80) (b)
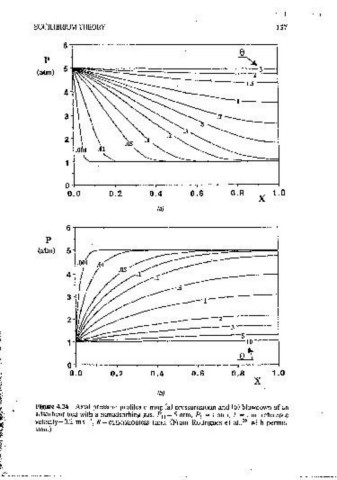
which was obtamed originally by Cheng and Hill. 37 In this situation, pressur- Figure 4.24 Axial pressure profiles dunng (a) pressunzat10:n and (b) blowdown of an
1zatton and blowdown are symmetnc processes. This symmetry 1s lost, how- adsorbent bed with a nonadsorbing gas. PH= 5 atm. PL= i atm, L = i m, reference
velocity-0.2 ms~•, O=dimensionless ttme. (From Roctngues et aJ., 36 with penms-
ever, when the pressure gradients are significant since the pressure response
s10n.)
1s then governed by Eo. 4.77, which 1s nonlinear. This 1s illustrated in Figure
4.24, which shows pressure profiles for pressunzatwn [Figure 4.24(a))