Page 205 - Pressure Swing Adsorption

;l.
!
182 PRESSURE SWING ADSORPTION DYNAMIC MODELING OF A PSA SYSTEM 183
l
10' ,-----------------------, 100 6b

40
g 95 ~
" C
0
§_
'--- .s " DiffusK>n model (constant D) "' g
~
·-··-··-· -~ C LDFmodel 30 ·1-
.n. 0 a
--·---·--···--·-->_- g 90 c
·c ~
>
20 0 u
*
10 e
0
0
::i: as *
10
'°o 100 160
0
Adsorption/desorpuon time (s)
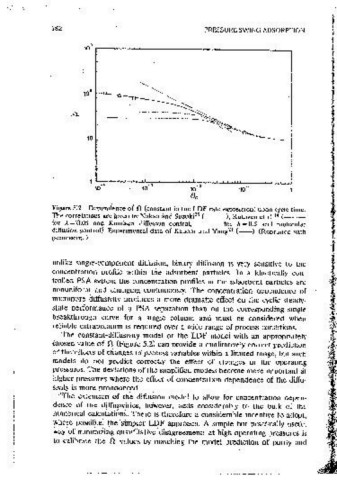
Figure 5.2 Dependence of .0 (constant in the LDF rate exPression) upon cycle time. Figure 5.3 Companson of the predictions of the diffusion ,and LDF models for a
The corre1at1ons are given by Nakao and Suzuki 35 (---.), Ruthven et'al. 14 (-- ·- Skarstrom PSA cycle showing the performance of two available correlations for
for A= 0.05 and Knudsen diffusion control, --·-- for A= 0.5 and molecuiar estJrnatmg the appropriate value of n as a function of cycle time. Pressur~
diffusion control). Expemnentai data of Kapoor and Yang 21 (--). (Reprinted with 1zation/blowdown timc=20 s, L/ooH=25 s, G=l.0, DA/rJ=3.73xI0- 1 s-i,
oermiss1on.) D 8 I r"z = 1.17x 10- 4 s~ . other parameters are same as m Table 5.8. (From
1
Ref. 26.)
unlike single-component diffusion, binary diffusion 1s very sensitive to the
concentration orofile within the adsorbent oarticles. In a kinetically con- recovery with limited exoerimental data for the reg10n of interest and then to
trolled PSA system th_e concentration profiles m the adsorbent particles are use these !l values to mvestigate the effects of the other ooeratmg variables ..
nonuniform and changing continuously. The concentration deoendence of Kapoor and Yang 21 used this approach m their study of kinetic separation of
m1cropore diffusivity produces a more dramatic effect on the cyclic steady- methane from a mixture of methane and carbon dioxide over a carbon
state performance of a PSA separation than on the corresponding smgle molecular sieve. Others 20 have used the constant-diffus1v1ty pore diffusion
breakthrough curve for a smgle column and must be considered when model with the diffus1v1ty values obtained by calibratihg the model against
reliable extrapolation ts reqmred over a wide range of process conditions. limited number of experimental runs. The constant-diffusivity m1cropore
The constant'diffus1v1ty model or the LDF model with an appropriately diffus10n model using calibrated effective diffusivit1es iS, however, no hctter
Chosen value·of n' (Figure 5.2) can provide a qualitatively correct prediction than a LDF model usmg the lim1ting diffusivity with the calibrated n. values.
of the effects of changes m pro<;;ess variables within a limited range, but such In view of the computat10nal efficiency, the latter approach appears prefer-
models do not predict correctly the effect of changes m the operatmg able. The lim1tatmns of the LDF model discussed here are, however, not
pressures. The deviations of the simplified models become more 1moortant at important for separations based on differences in adsorption equilibrium. For
higher pressures where the effect of concentration dependence of the diffu- this class of separations, the LDF moctei approach 1s adequate m almost all
sivity is more pronounced. situations.
The extens10n of the diffuSion model to allow for concentration depen-
dence of 'the diff~sivities, ho·wever, adds considerably to the bulk of the
numerical calculations. There is therefore a considerable incentive to adopt, 5.1.4 Numerical Methods
where possible; the simpler LDF approach. A simple but practically useful Even the simplest PSA model including mass transfer resistance is not
way of m1mmiZing Quantitative 'disagreements at high ·operating pressures is amenable to anaiytic solut10n, and efficient numencal methods for solving the
to calibrate the !1 values by matching the model prediction of punty and coupled partial differential equations are therefore needed to solve 1he